展開の公式（乗法公式）の計算方法を図にしてみました

中学3年生で習う展開の公式ですが、数学は決して苦手じゃないはずなのにこの公式を使わず、いちいち分配法則で計算している……というケースをたまに見かけます。さすがにそれはもったいない！ということで、解き方を図にしてみました。

教科書には乗法公式4パターンがaやbを使った数式の形で載っているのですが、それを見て「へぇ、こうやって計算するんだ」とすんなり理解するのは難しいので、なるべくビジュアル化してお伝えしたいと思います。

基本4公式

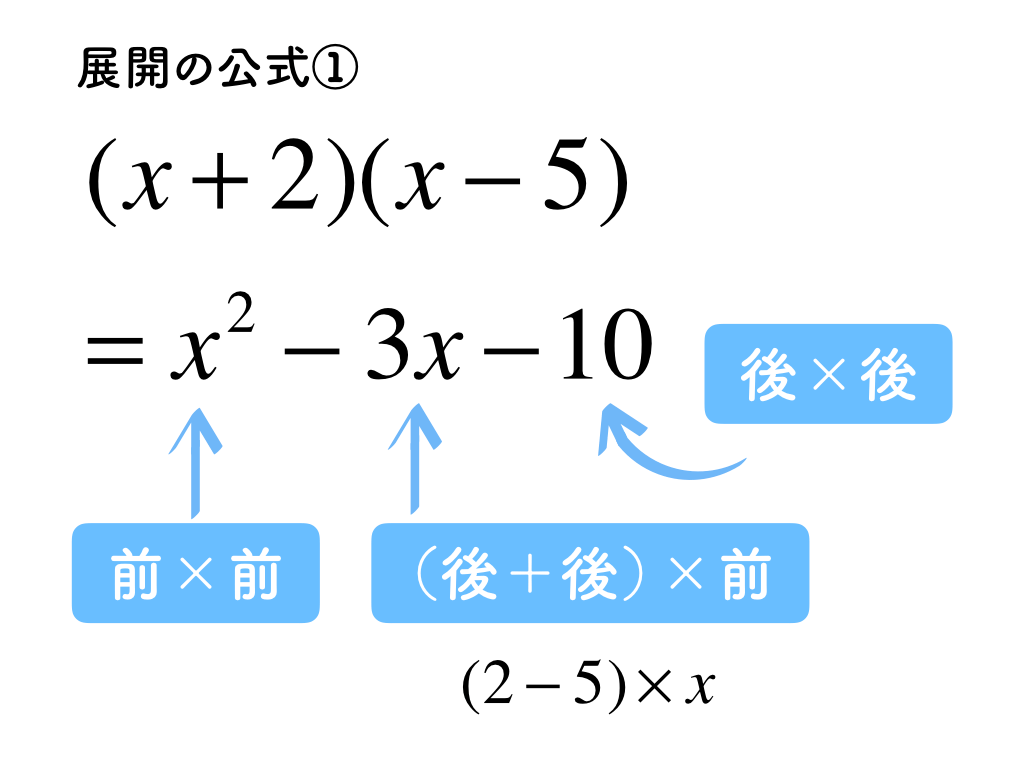
公式は4つあるものの、基本的にすべて最初の公式のマイナーチェンジ版でしかありません。真ん中の項は足し算、最後の項はかけ算です。「後ろどうし足して-3、かけて-10」と手際よく計算していきましょう。

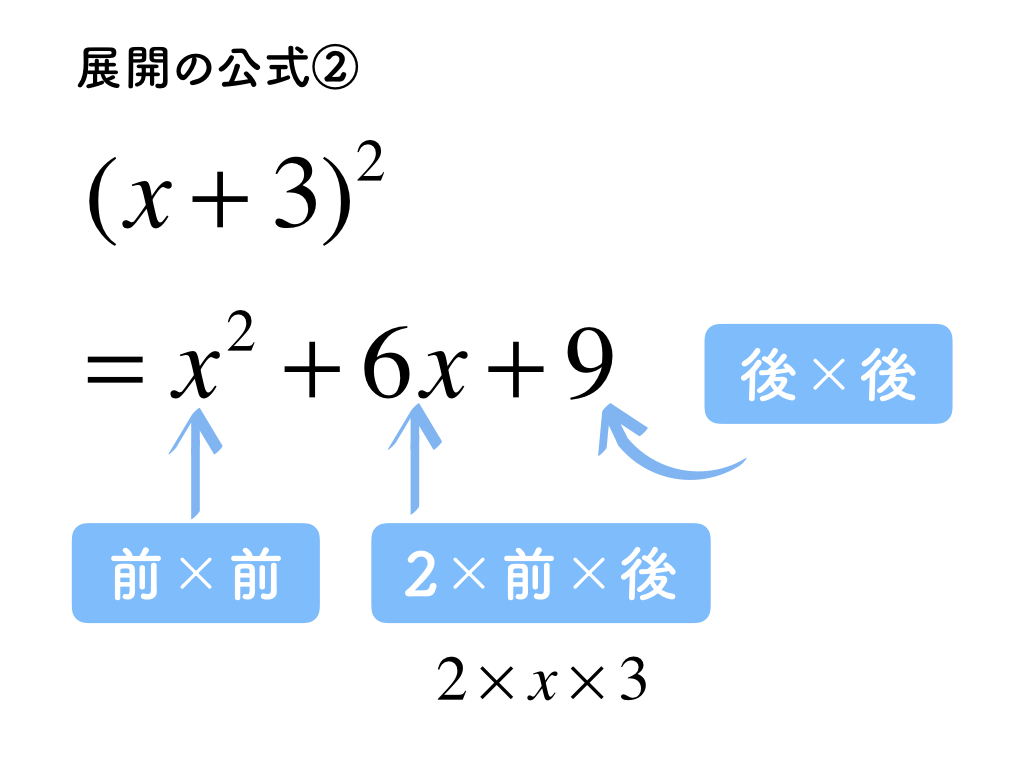
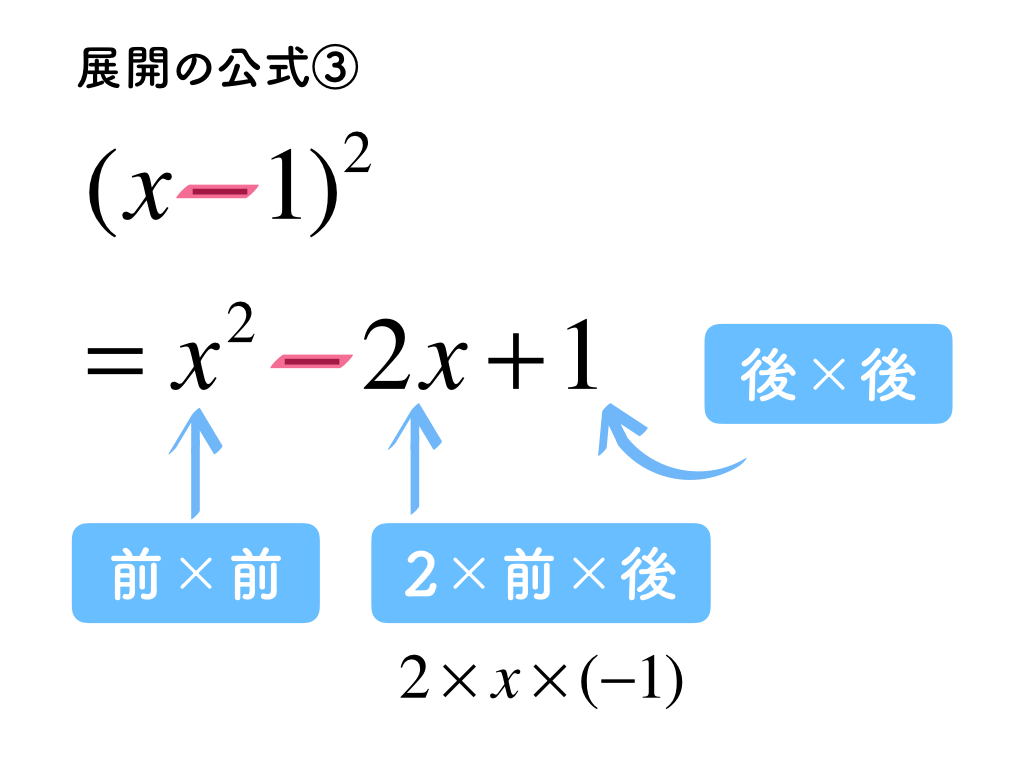
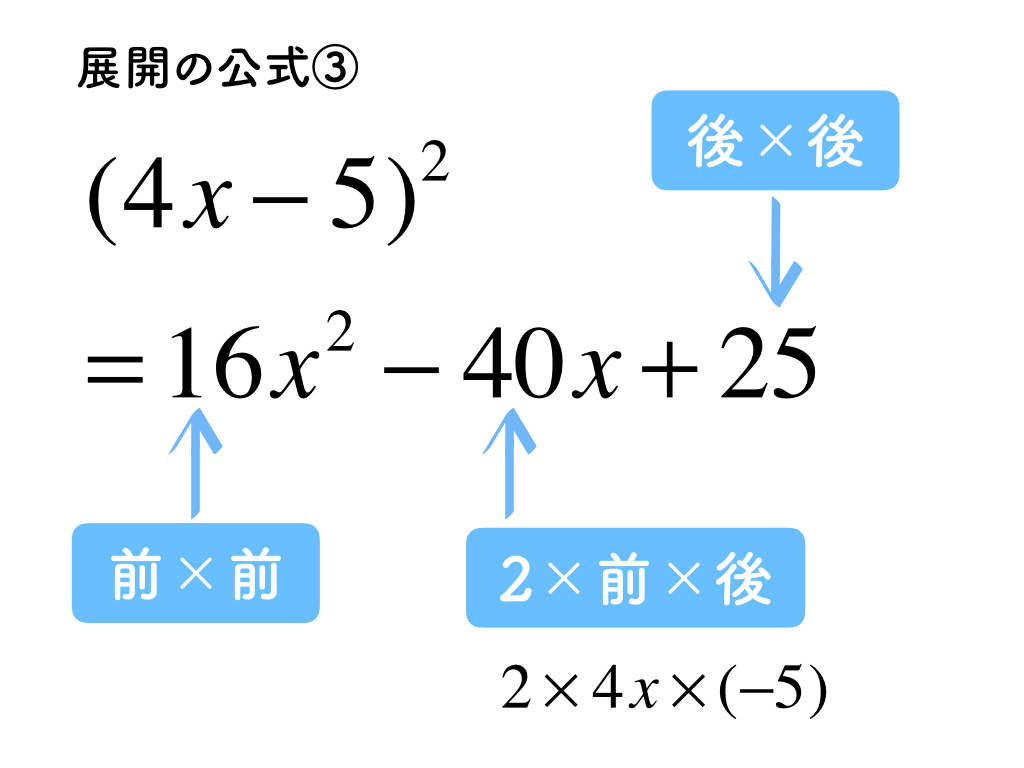
2・3番目の公式はいずれも2乗が出てきます。この公式をうまく覚えられなければ、2乗をバラして(x+3)(x+3)と2つ並べ、最初の公式に当てはめて「足して6、かけて9」と計算してしまうのもアリです。そして、慣れてきたら公式通り解けるようにチャレンジしてみて下さい。

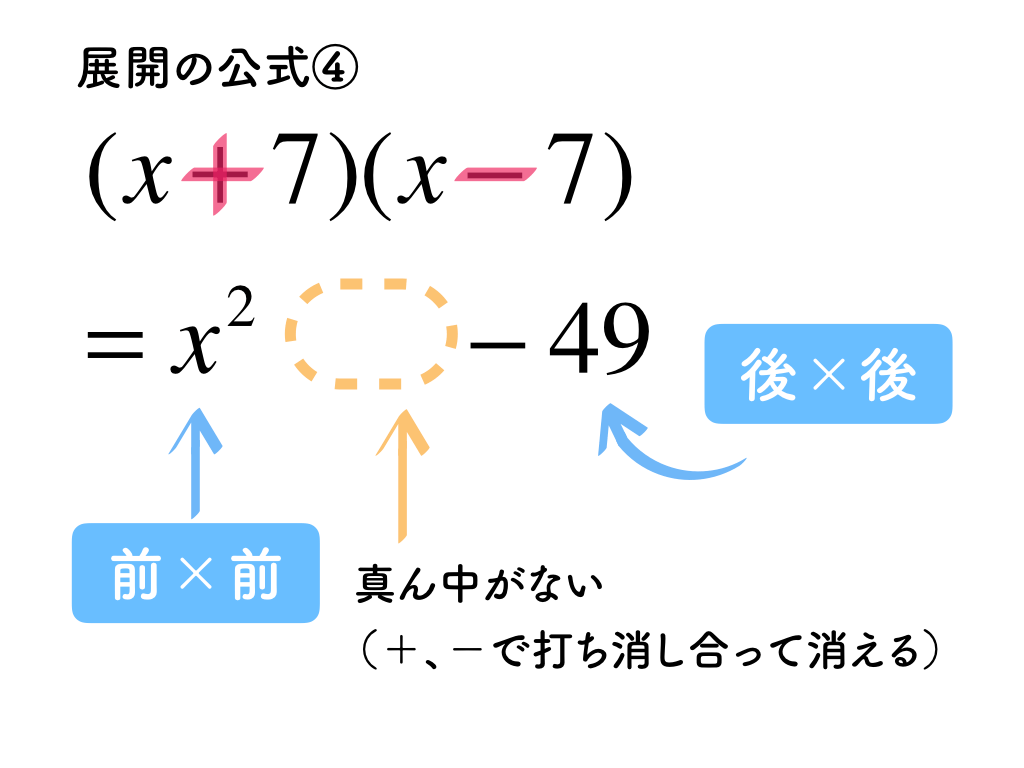
最後の公式は数字部分が同じで、符号部分はプラスマイナスで互い違いになるバージョンです。他の公式と異なり、真ん中の項がありません。足し算するとプラスとマイナスで消えてしまうのです。

先ほどのパターンはすべて文字が1種類だけでしたが、次は文字が2種類出てくるパターンです。まず、文字がどこに何個出てくるか、その形を覚えてしまいましょう。

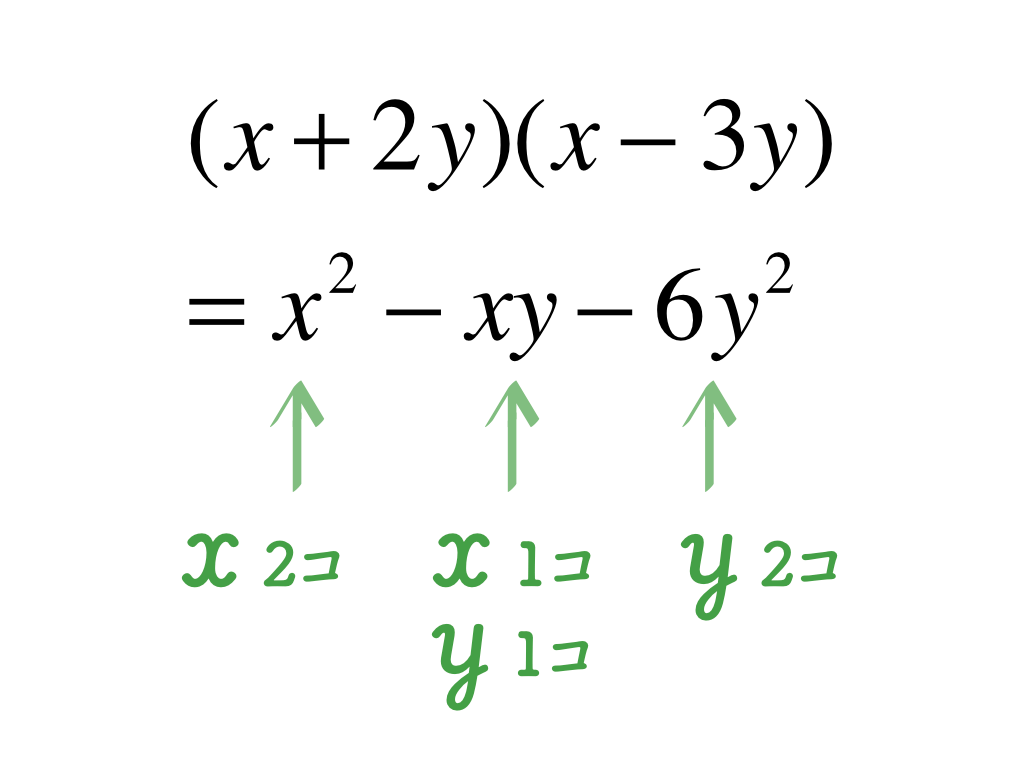
左から右に行くにつれ、xの個数（次数）は減り、yの個数が増えていきます。この形を暗記しておけば、あとは数字の計算に集中できます。

最初の文字の前に数字がある場合（係数が1以外）です。内緒の話、数学の苦手な受講生に対しては「このパターンの計算は公式を使っても大して楽にならないから、一個一個分配法則して計算してもいいよ」と言っています。でも、できれば是非ともマスターして、瞬時に答えを出せるようになれば時間短縮できます。

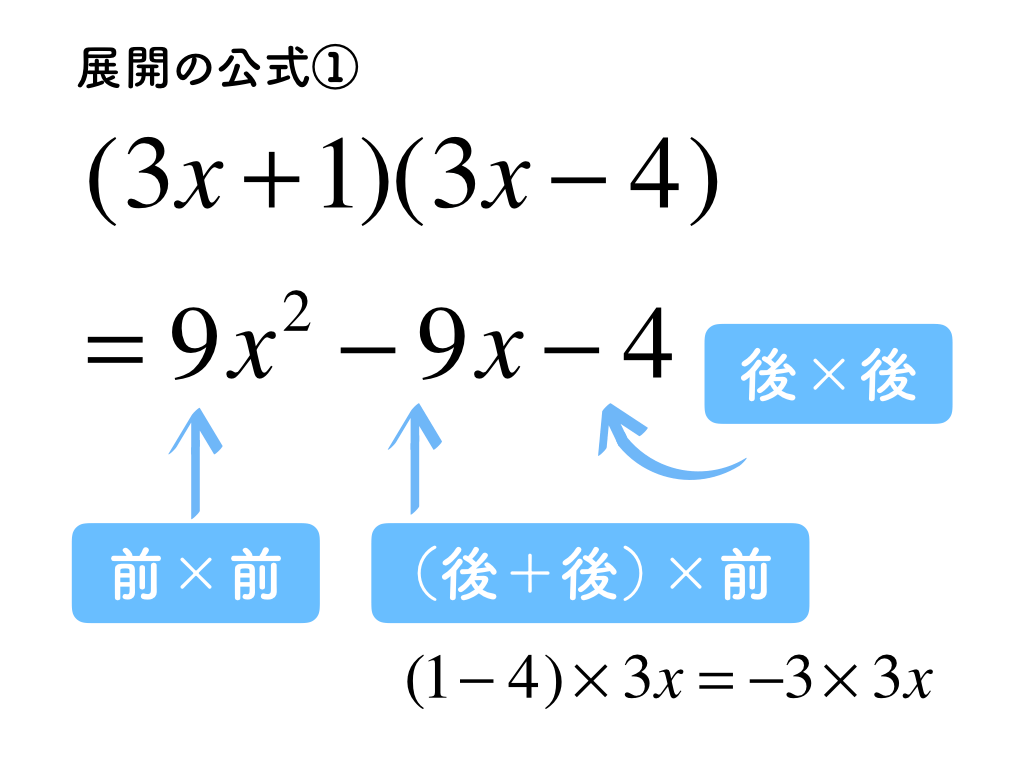
最初と最後の項は特に問題ないはずです。真ん中の項の計算に気をつけましょう。「後ろどうし足して、前とかける」という手順です。

もう一つだけ例をお見せしたいと思います。こちらもやはり真ん中の項に注意。