平方根はなぜプラスとマイナス両方あるの?ルートの基本を確認
平方根の計算は、中学3年生で学習する多くの分野との関連がありますので(方程式・関数・図形……)、最初に基本的なイメージをがっちりつかんでおくのが大事だと思います。例えば、「9の平方根は?」などといきなり質問されたとき、迷わずに「±3だよ」とスパッと答えられるでしょうか。なぜプラスマイナスが必要なのか、図をご覧ください。
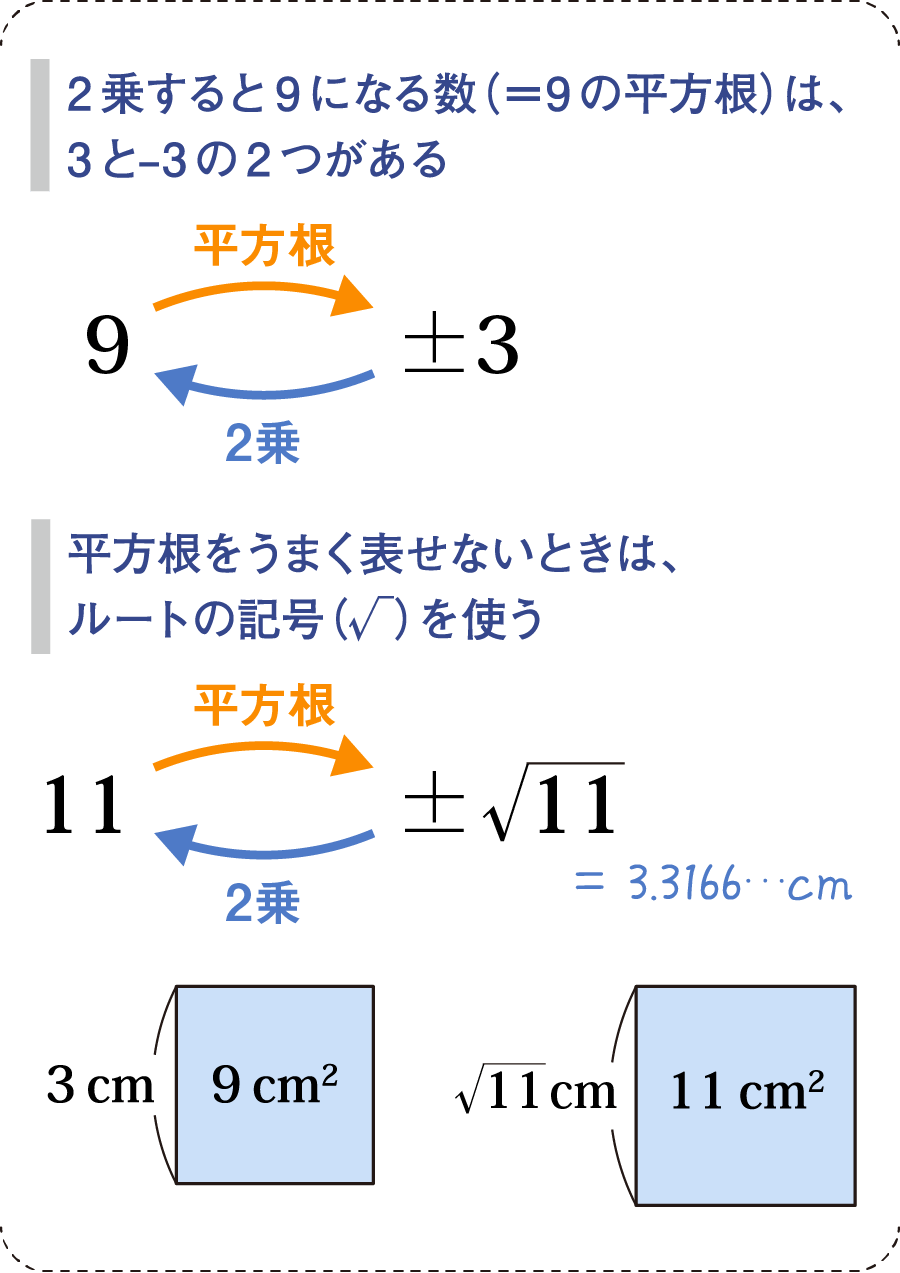
このように、ある数の平方根にはプラス・マイナスの両方があります。「9の平方根は?」と聞かれたら、「何を2乗したら9になるの?」と質問されているのと同じです。この場合、プラスの3はもちろん、マイナス3も2乗すれば9になります(マイナス×マイナスでプラスに)ので、両方とも答えにしていく必要があります。
ところで、平方根はきれいな数にならないことが多いです。電卓の√ボタンを押してみればわかりますが、例えば3の平方根は±1.73205…という無限に続く小数で、しかも数字の並びは規則性がなくバラバラです(無理数といいます)。こういう数字を紙に書いていたらキリがありませんから、そのときは根号(√の記号)の出番となります。
ルート付きの数字を見たときは、とりあえず正方形を思い浮かべるようにしましょう。例えばルート11は、面積が11である正方形の1辺の長さとなります。
そして、根号についての以下の計算は、これから当たり前のように使っていきますので慣れておきましょう。このときも正方形のイメージが重要です。

1, 4, 9, 16, 25……といった、自然数の2乗になっている数の並びに注目です。図には載せませんでしたが、これを使ってルートの中身の大ざっぱな予測をすることができます。
- ルート45……ルート36とルート49の間だから、6と7の間の数
- ルート80……ルート64とルート81の間だから、8と9の間の数
- ルート81(=9)の手前なので、9より少しだけ小さい数と考えることもできる
次に、0がたくさん並ぶ、ケタ数が多い数のルートについてです。根号を外せるかどうかの見極めが大事です。
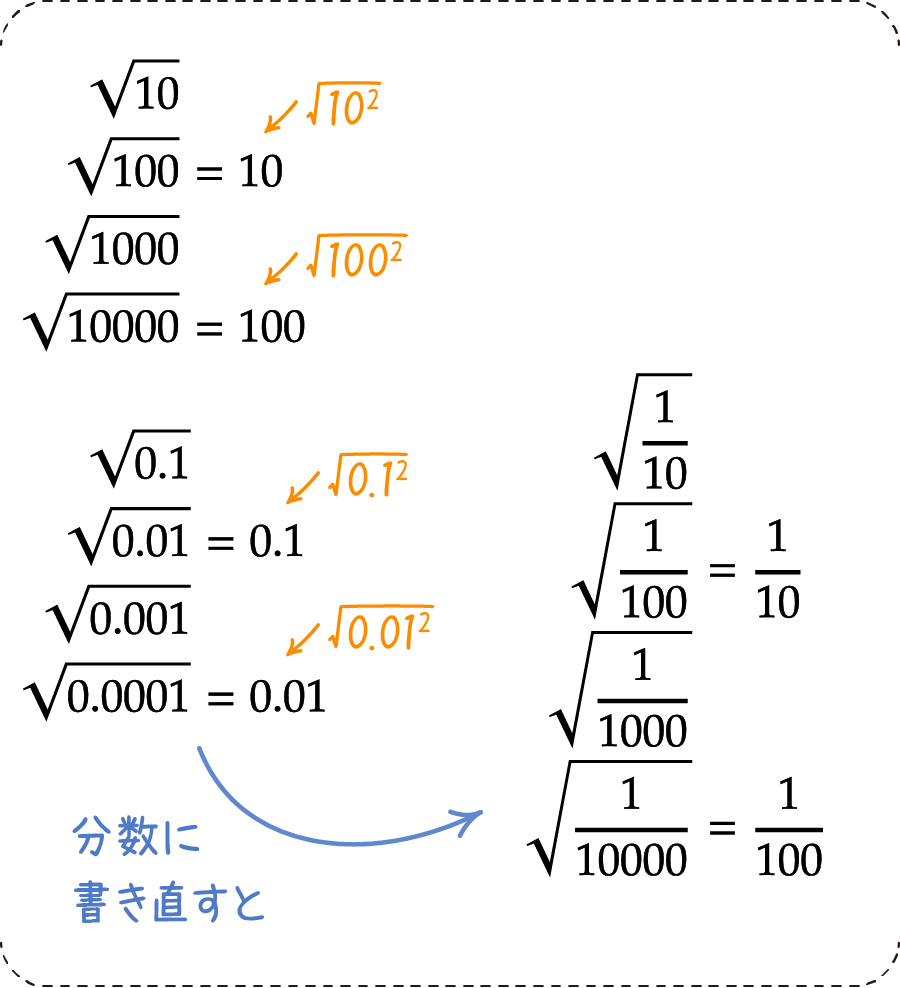
このあたりはまだわかりやすいですが、下のような数字になるとちょっと迷ってしまうかもしれません。掛け算の筆算方法も一応載せておきましたので、確認してみて下さい。
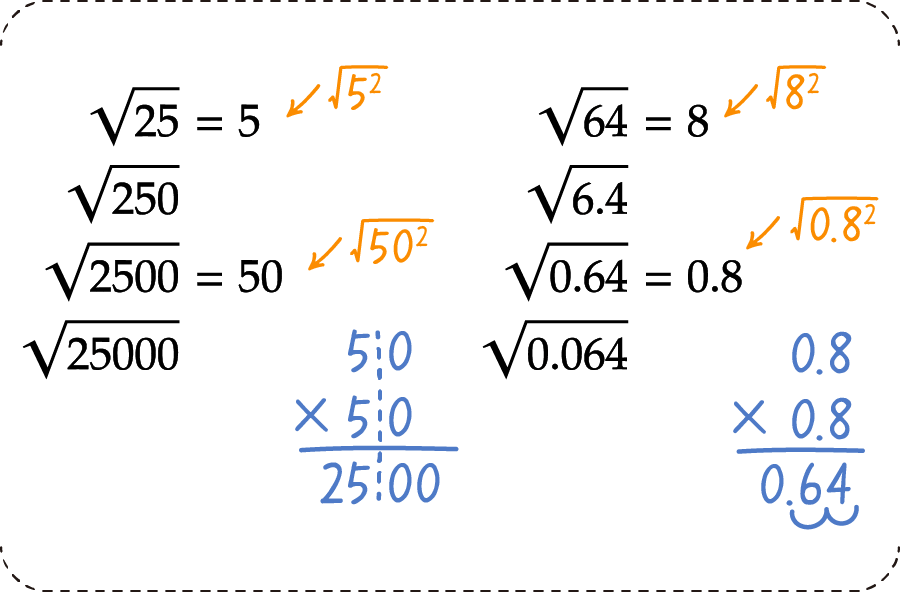
この記事は、平方根について習いたての方を念頭に置いています。もう少し学習が進んでいる方は、「ルートの中身を小さくする問題」の記事もご覧下さい。