小学校の分数【後編】 – かける・わる

このページでは、小学校で学習した分数のかけ算・わり算の復習を扱っていきます。通分をしたり小数に変換したり、といった分野については、分数計算前編のページをご覧ください。

この辺りは、そもそも「なぜかけ算・わり算になるか」というイメージがわきにくいところでもありますので、図表を使った解説を心がけてみたいと思います。

分数のかけ算のイメージ

かけ算は、「1あたり」の量があらかじめわかっていて、この量を引き伸ばしたり縮めたりするときに使います。例えば、次のような場合が代表例です。

• 1kgあたり300円のみかんを2kg買ったときの値段は？
• 1mあたり3kgの鉄パイプを3分の2にカットしたときの重さは？
  以下は、みかんの値段について、分数のかけ算のイメージを図表にしたものです。

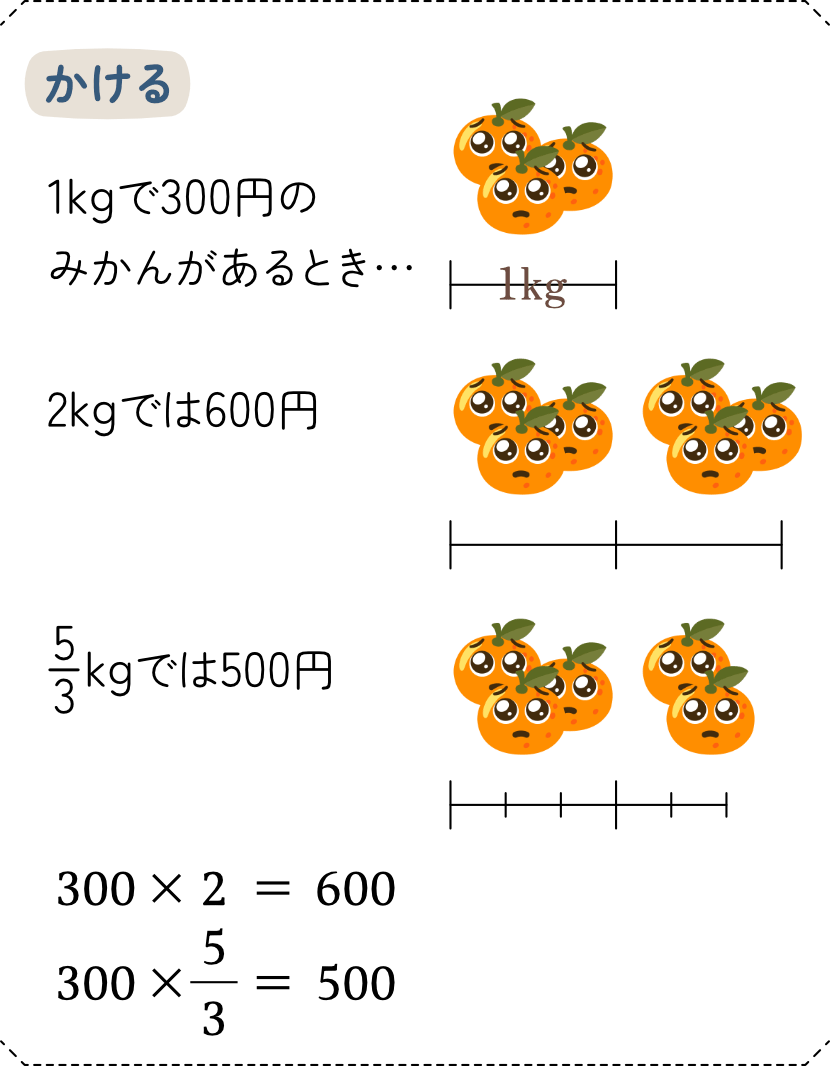
かけ算の計算方法

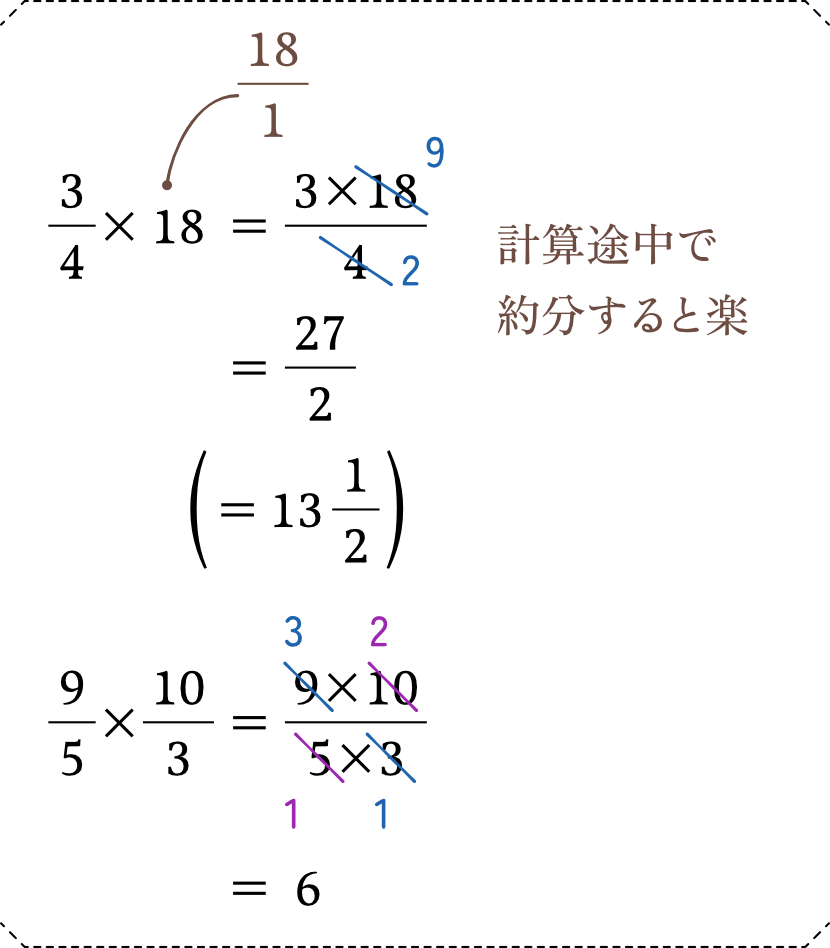
分数のかけ算の場合、たし算ひき算と違って通分のような作業は必要ありません。そのまま分子・分母同士をかけ算すれば大丈夫です。

かけ算・わり算は計算途中での数字の約分が可能です。最後に約分をするやり方でも一応答えは出てきますが、計算途中、あまり数字が大きくならないうちに約分をしておくと楽に答えを導けます。

分数のわり算のイメージ

分数のわり算は特にイメージがつかみにくいところです。「みかん1kgあたりの値段」「鉄パイプ1mあたりの重量」のように、「1あたり」の量を求めるときにわり算が役に立ちます。

わり算の計算方法

分数のわり算は、分母分子をひっくり返した「逆数」のかけ算によって計算することができます。整数は、図の通りいったん「1分の○」という分数に直してから上下をひっくり返すことになります。

これを実際の計算に当てはめると、次のようになります

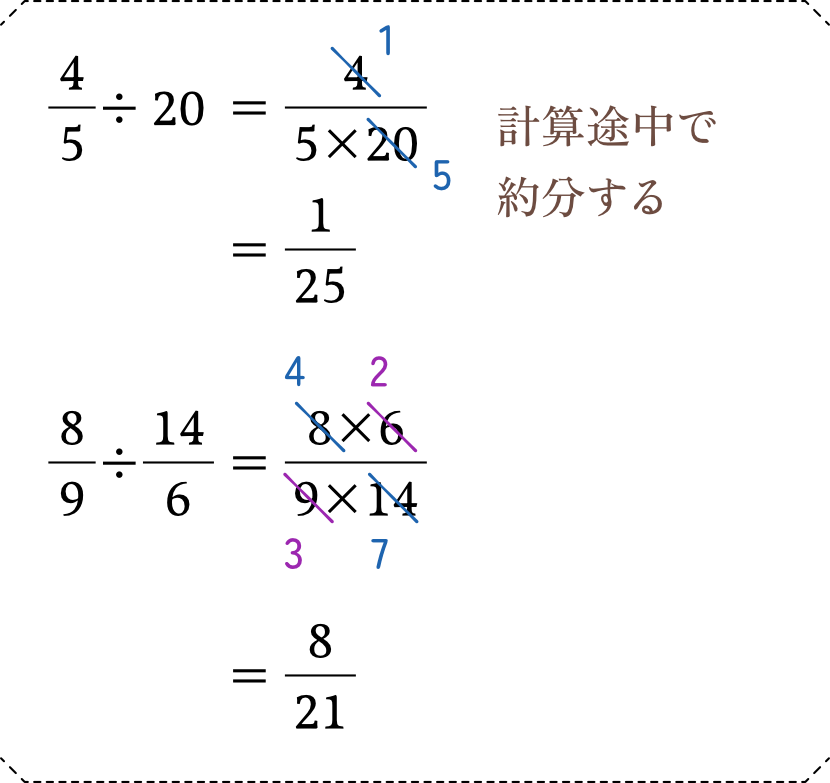
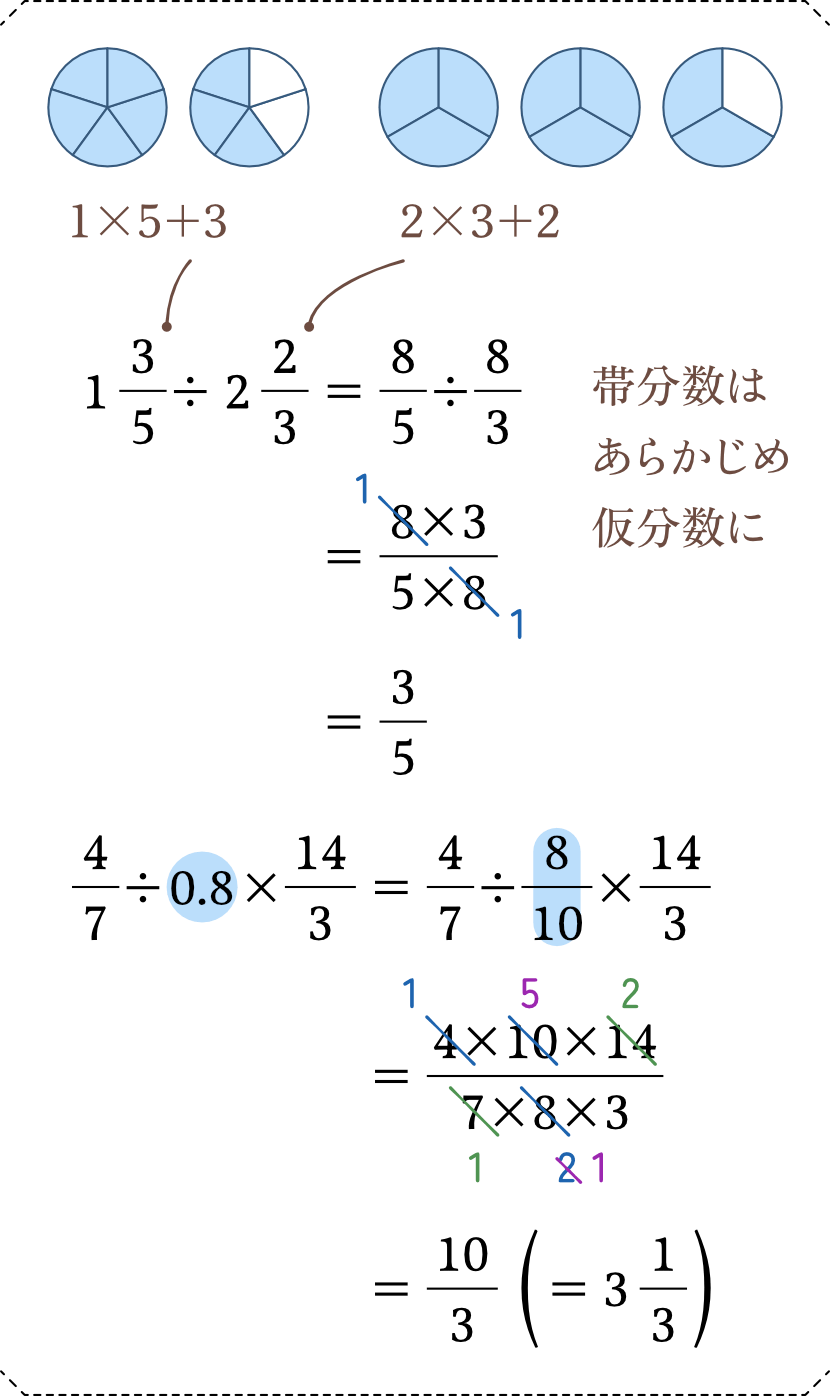
少しむずかしめの計算

帯分数の場合は、いきなり計算しようとせずに、仮分数に直してから計算する必要があります。また、小数・分数の両方を含む計算の場合、小数を分数に直しておく必要があります。詳しいやり方は、前編のページも参考にしてみてください。分数を小数にしてしまうと、わり切れず正確に数を表すことができないので、分数に揃えます。