小学校の分数【前編】 – 通分約分・たす・引く・小数分数変換

分数計算は独自のテクニックが多いため、小学校の学習事項のうちわかりにくいものを、2回に分けて一気にご紹介します。ここでは通分約分や、たし算引き算に関連する問題を取り扱い、かけ算わり算は後半のページで取り上げます。

このページは分数の苦手な中学生を想定しているため解説があっさり目ですが、小学生の復習用としても使えるように作ってあります。

帯分数、仮分数の変換

分数の大きさを大まかに知ることができるのが「帯分数」ですが、実は中学校以降ほとんど使わず、すべて仮分数で表すことになります。でも、帯分数は分数のイメージをはっきりさせるのに役に立ちますので、基本的な計算はできるようにしておきましょう。

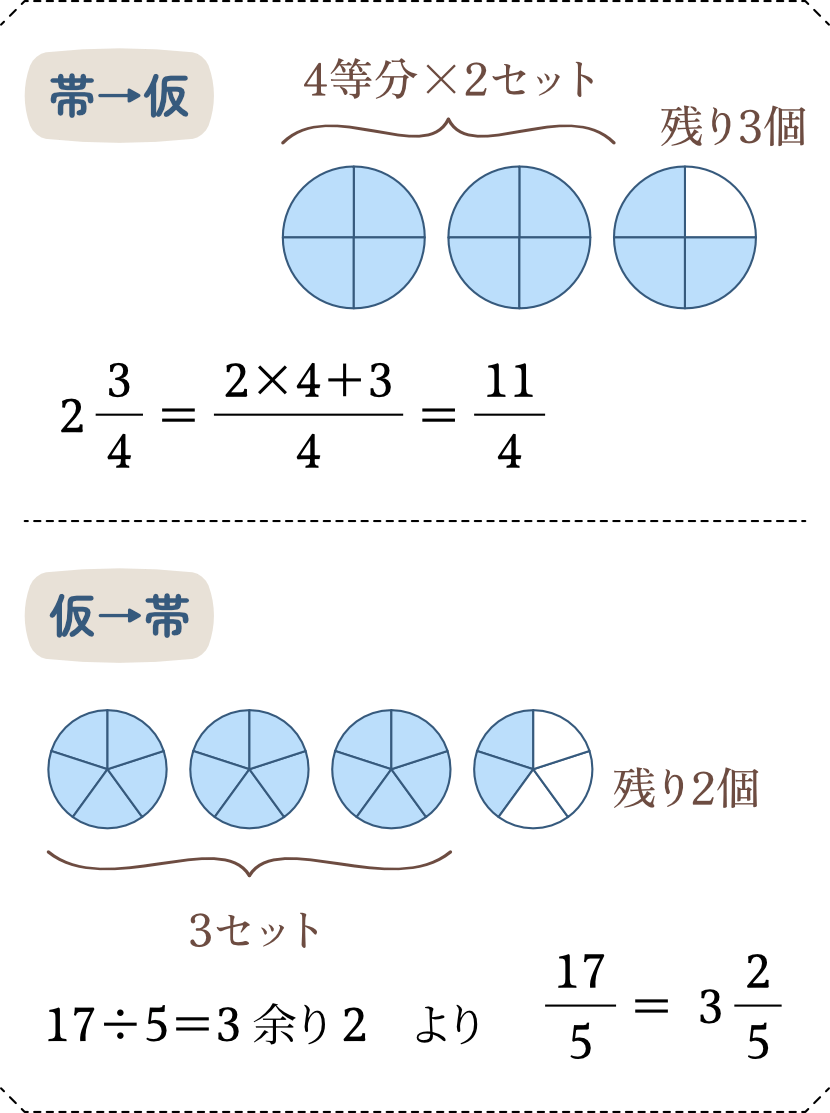
例えば「4分の○」という分数だったら、4個ずつのカタマリを作っていくことを意識するとよいと思います。

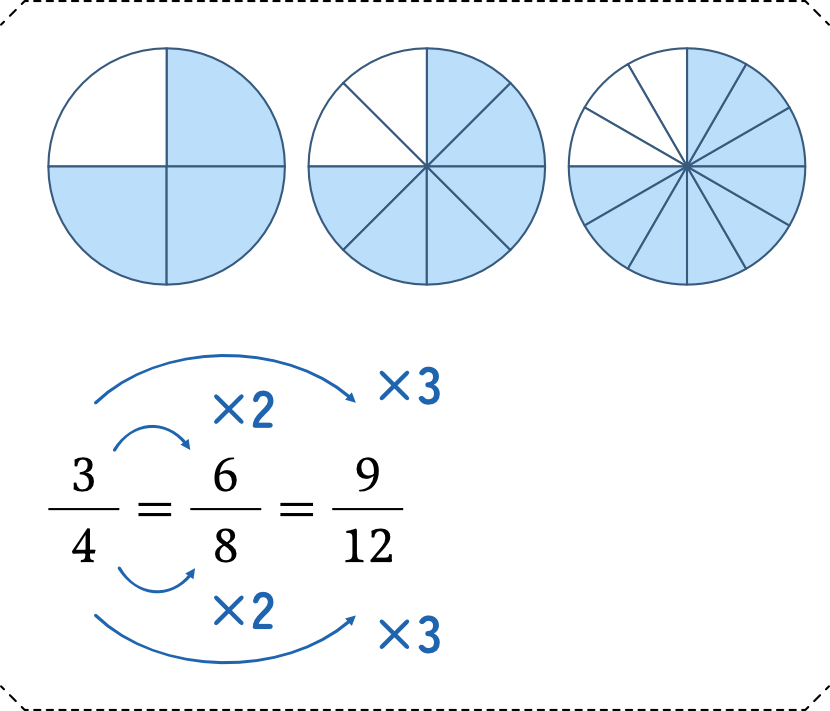
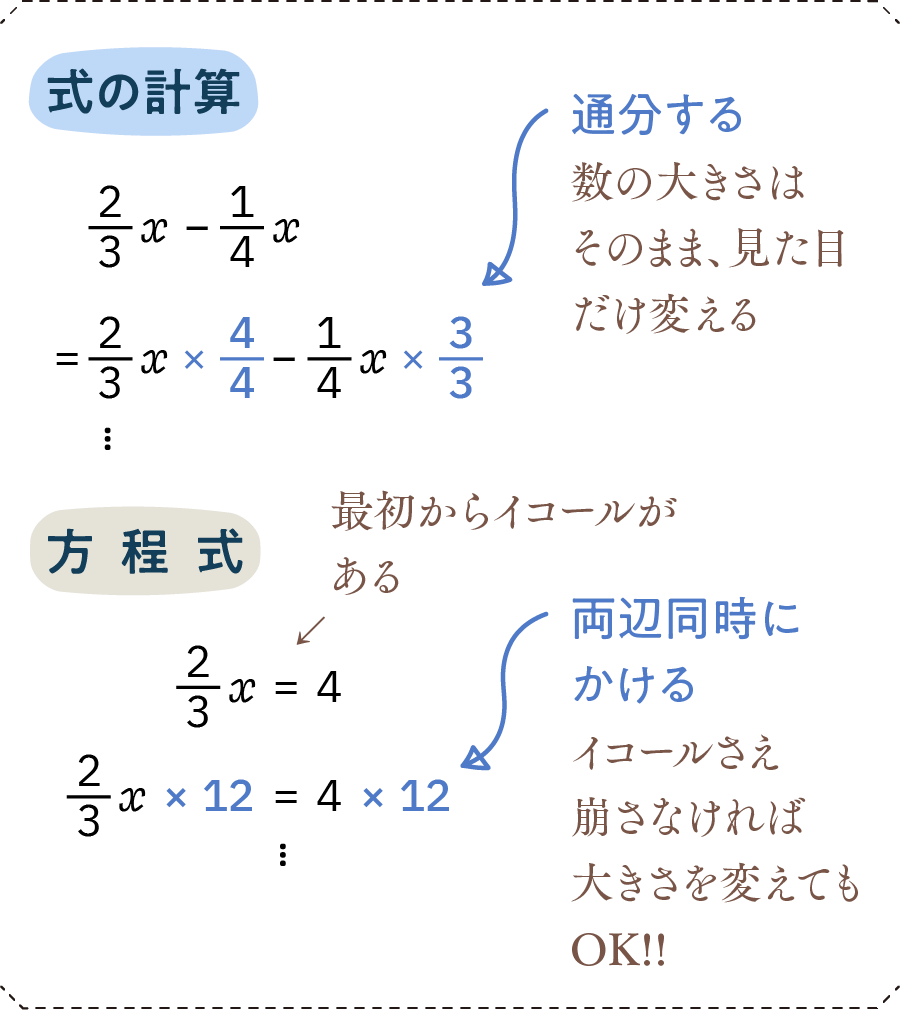
分数の分子と分母両方に同じ数を掛け算すると、分数の大きさそのものは変わらず見た目だけを変えることができます。これはすぐ後に出てくる「通分」で必要となるテクニックです。

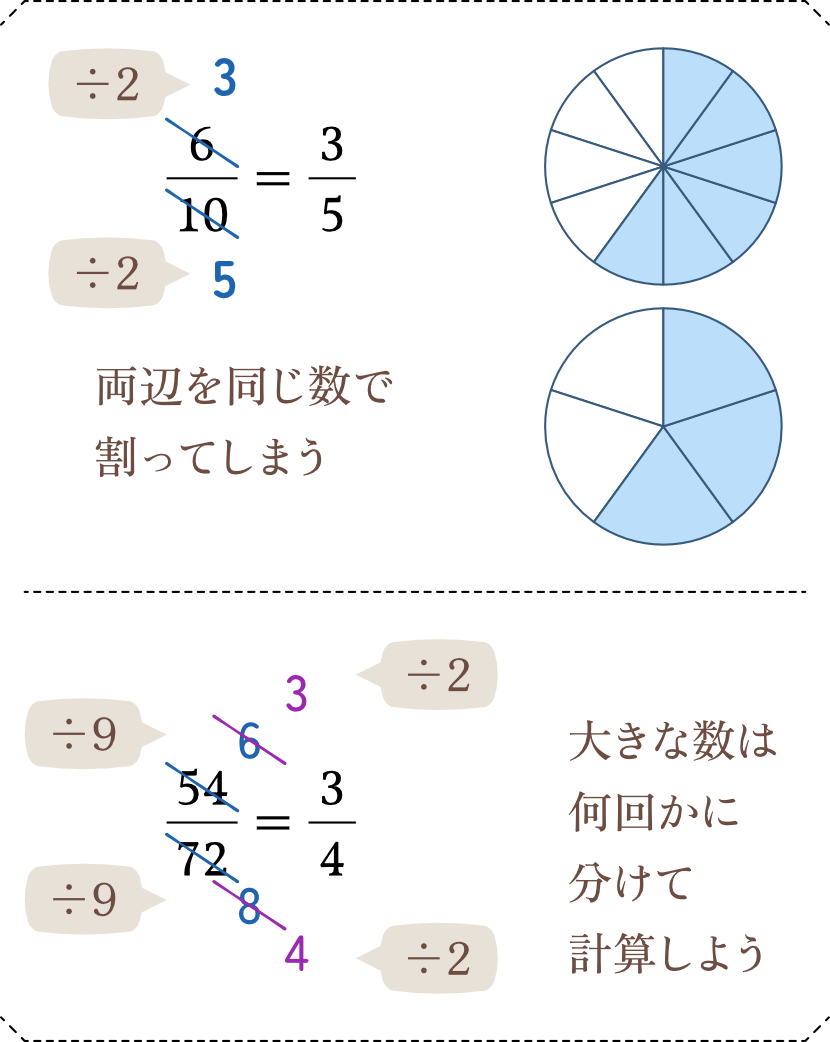
先ほどとは反対に、分子と分母で同じ数の割り算をすることで、分数の見た目をスッキリさせることができるのですが、これが「約分」です。分数計算をするとき、約分できるときは必ずしなければなりません。

下の例のように分数の数字が大きい場合は、1度で一気に約分しようとせずに、何回か細かい割り算を繰り返すことをおすすめします。

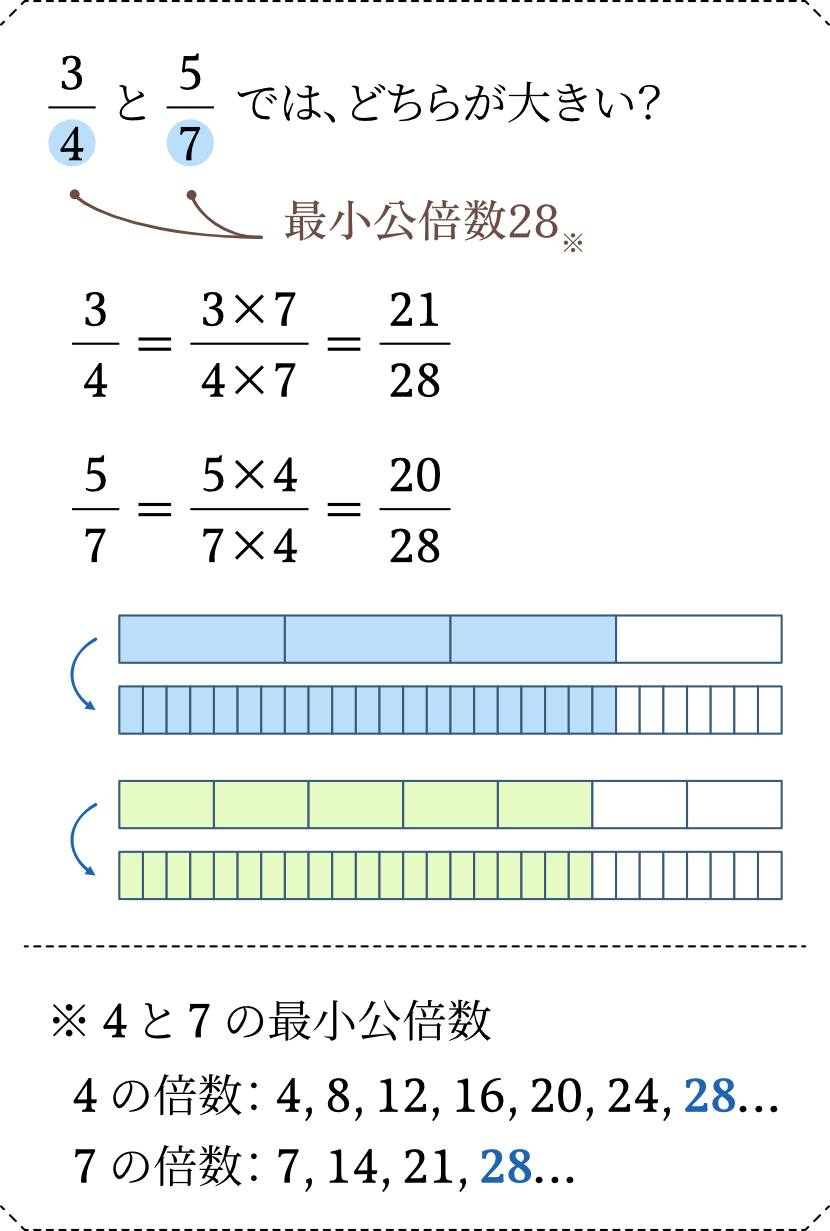
分母の異なる分数で大小を比べたり、足し算引き算をしたりする場合は、まず分母を揃える「通分」の手順が必要です。では分母を何に揃えるか？これは2つの分母の「最小公倍数」となるのですが、ちょっとイメージしにくいかもしれません。

例えば「4分の○」と「7分の○」という分数だったら、4の倍数と7の倍数、乱暴に言えば4の段と7の段の両方にある九九の数字で、一番小さいものは何だろうというのを考えてみると良いかと思います。

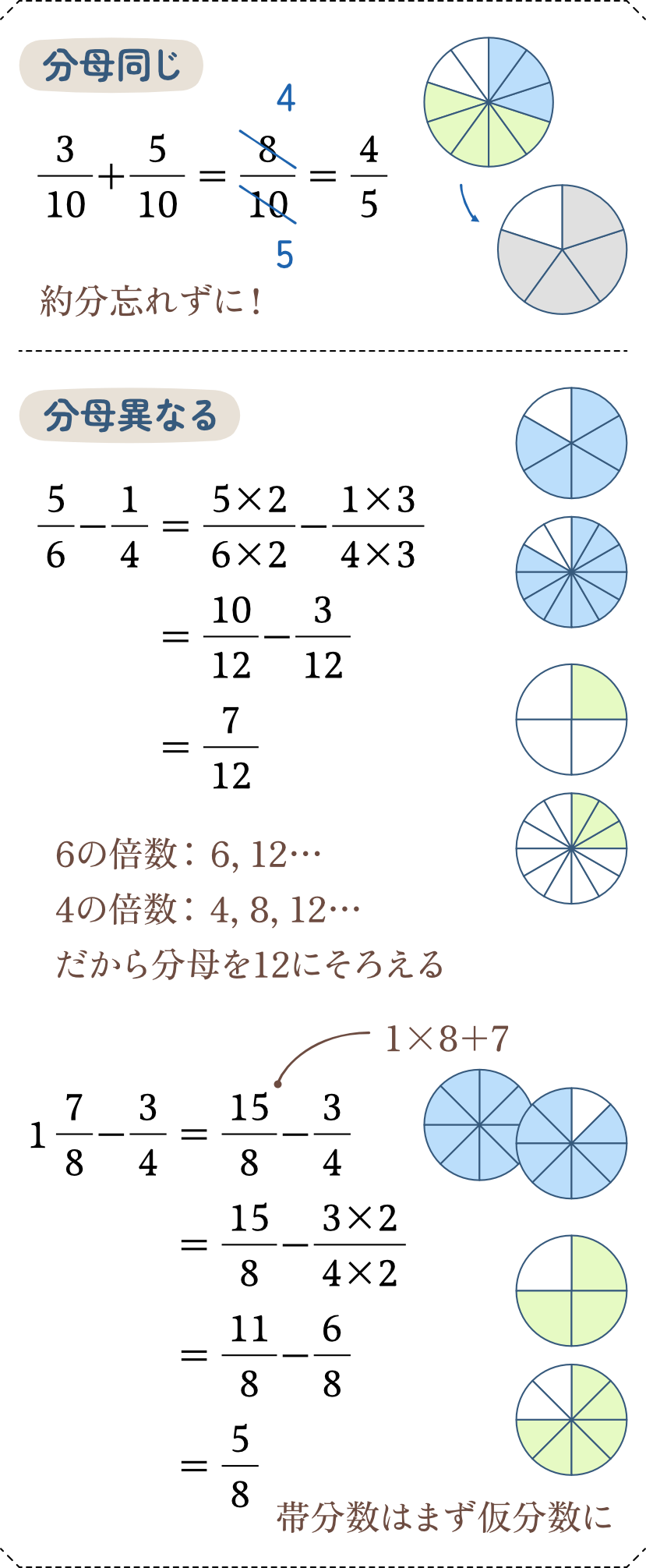
分数が同じ分母どうしであれば、分子部分のみ足し算します。約分をお忘れなく。
分母が異なる場合は、通分が必要になってきます。

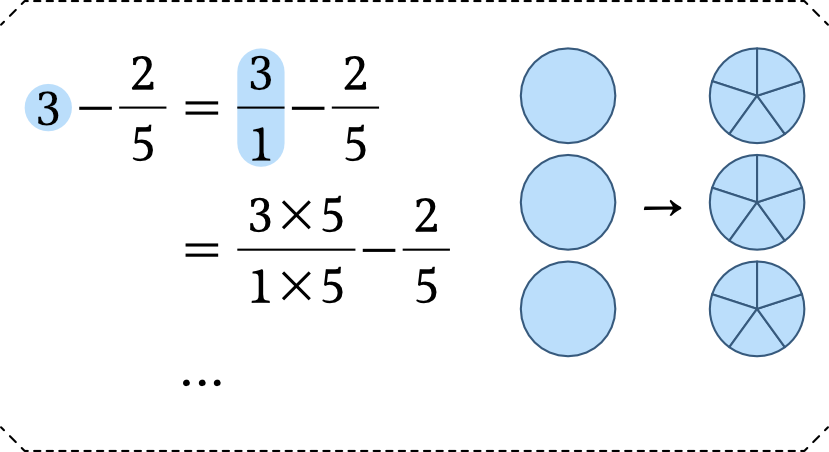
整数と分数が同時に出てくる計算の場合、整数を分数に直して形を整えます。整数は「1分の○」という形の分数に変形できますので、あとは必要に応じて通分すればOKです。

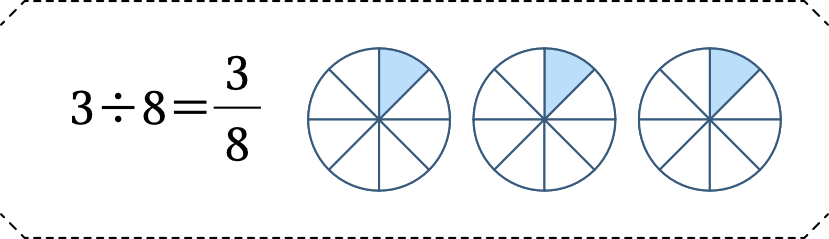
3枚のピザを8人で切り分けるとき、どう分配したらよいでしょうか。一番シンプルでわかりやすいのは、それぞれピザを8等分して、カットしたものを3ピースずつ持っていく方法ではないでしょうか。このように、割り算は分数の形で表すことができます。

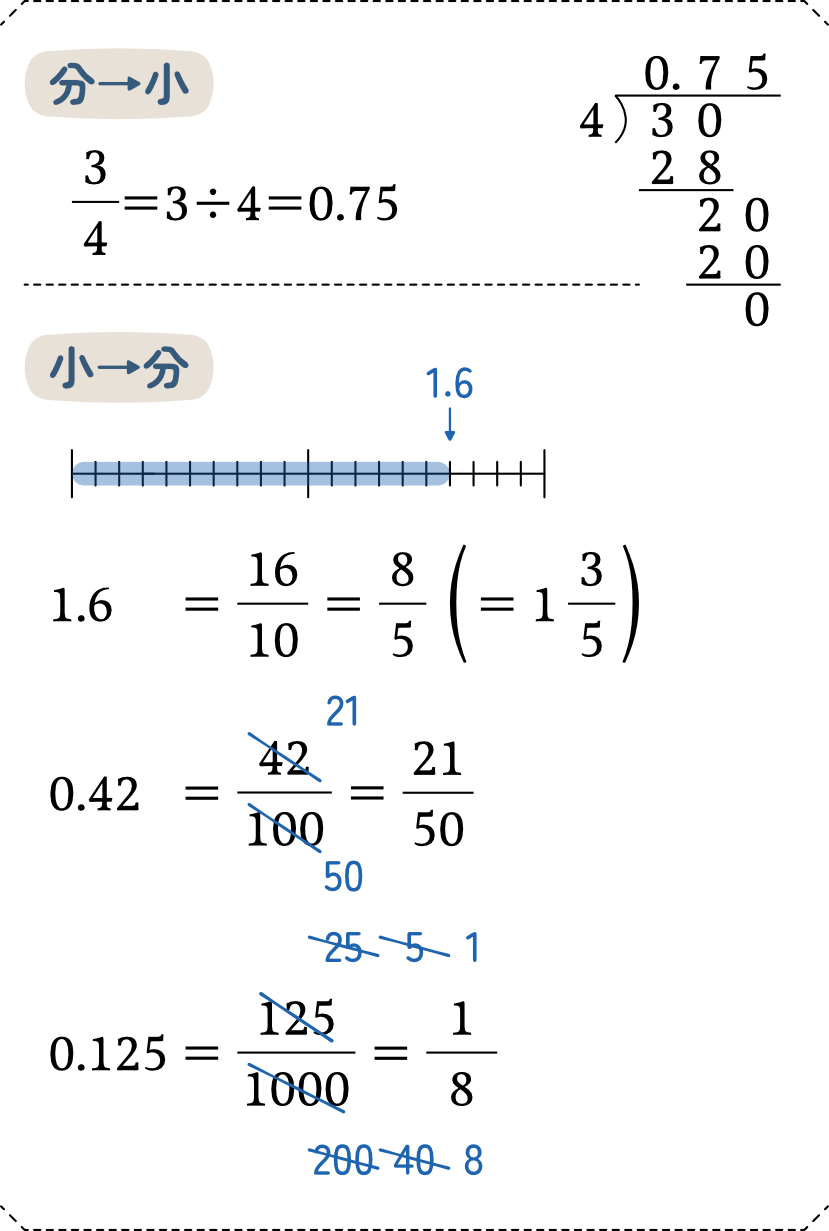
分数を小数に直すためには、いったん割り算を経由させます。これによって、分数の大体の大きさを知ることができます。

次に、小数から分数への変換についてですが、小数点の位は小数第一位なら「10分の1の位」、小数第二位なら「100分の1の位」と表現できることを覚えているでしょうか。これを利用して分数に直していきます。

小数でよく出題されるのは「4分の○」を表すものです。0.25きざみの数字となりますが、そのまま丸暗記しておいた方がよいでしょう。