等式変形（〜について解く）は、移項に注意

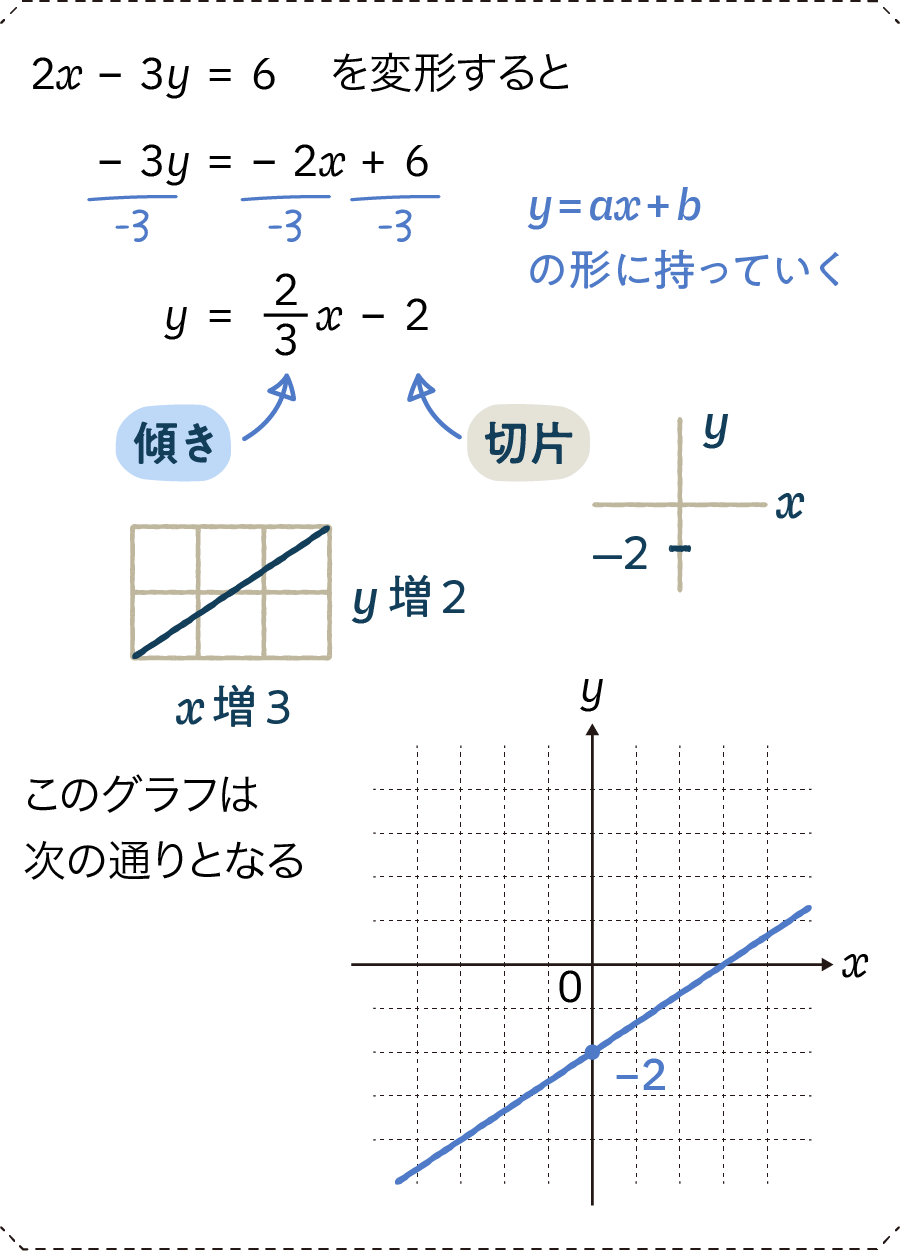
等式（すでにイコールがついた式）を変形させる「等式変形」についての解説です。例えば、辺の長さから面積を求める式を組み替えて、面積から辺の長さを求める式へと変化させることができます。

この単元は、計算の苦手な人だと本当に手も足も出ないという状況になりがちですので、一般のテキストだと省略してしまいがちな細かい計算もビジュアル化してみました。

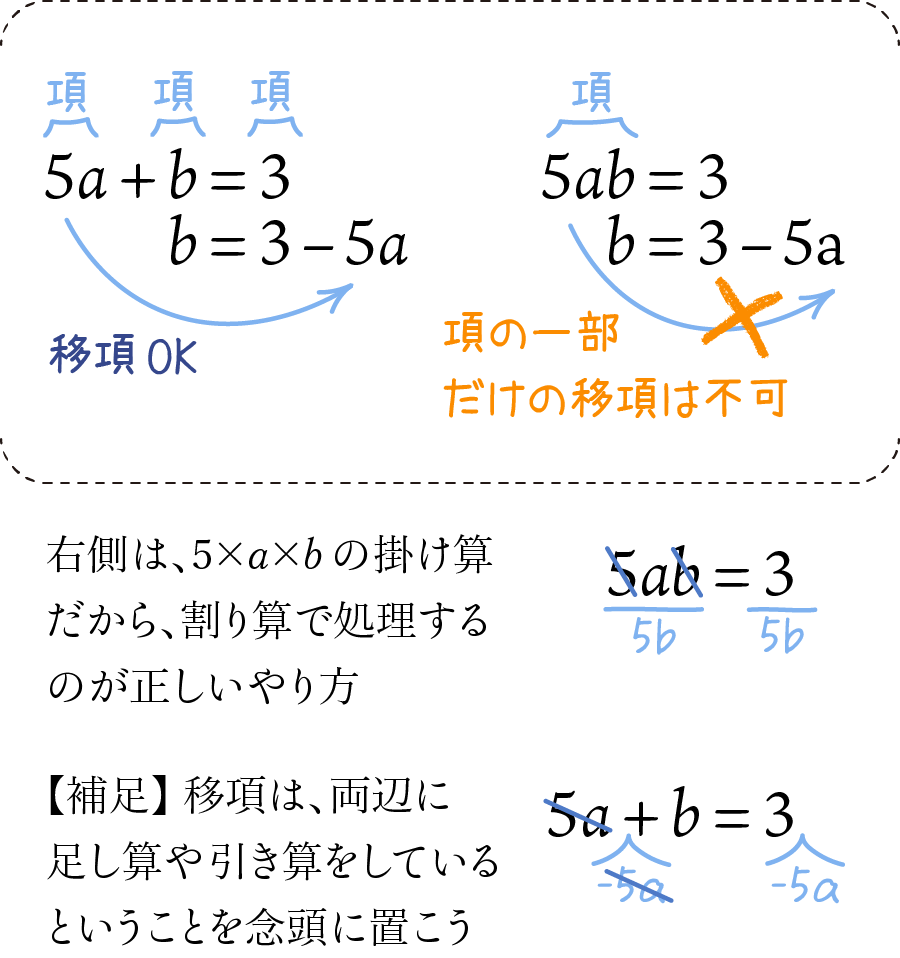
移項できる？できない？

例題のご説明に入る前に、項を左右に移し替える「移項」について、できるパターンとできないパターンの違いを確認しましょう。特に単項式の計算で、図の右のような計算をしてしまう（項の中の一部だけを引きちぎることはできないんです！）人が多いのですが、絶対にやって欲しくない間違いです。

3つの例題を確認

それでは、具体的な問題の解き方を見てみましょう。

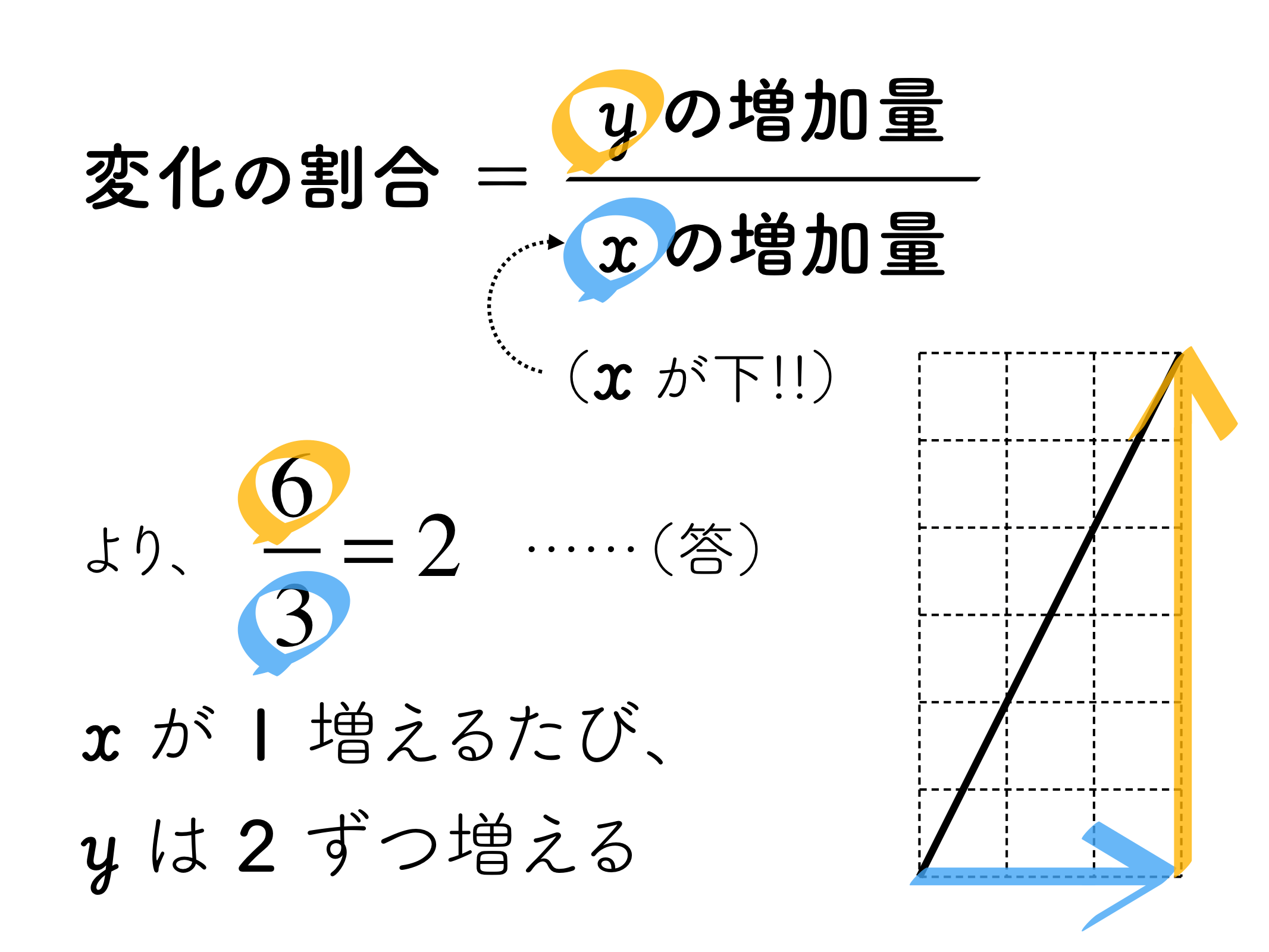
【例題1】 よく見るパターン

まずは一番基本的な、移項を利用して整理する方法です。一番よく目にするパターンだと思います。

【例題2】 単項式だけのパターン

次の問題のように単項式しか出てこない場合、移項という作業は出てきません。かけ算・割り算だけで処理していきます。この問題になるとガクッと正解率が下がりますので、マスターできればテストの点数も安定すると思います。

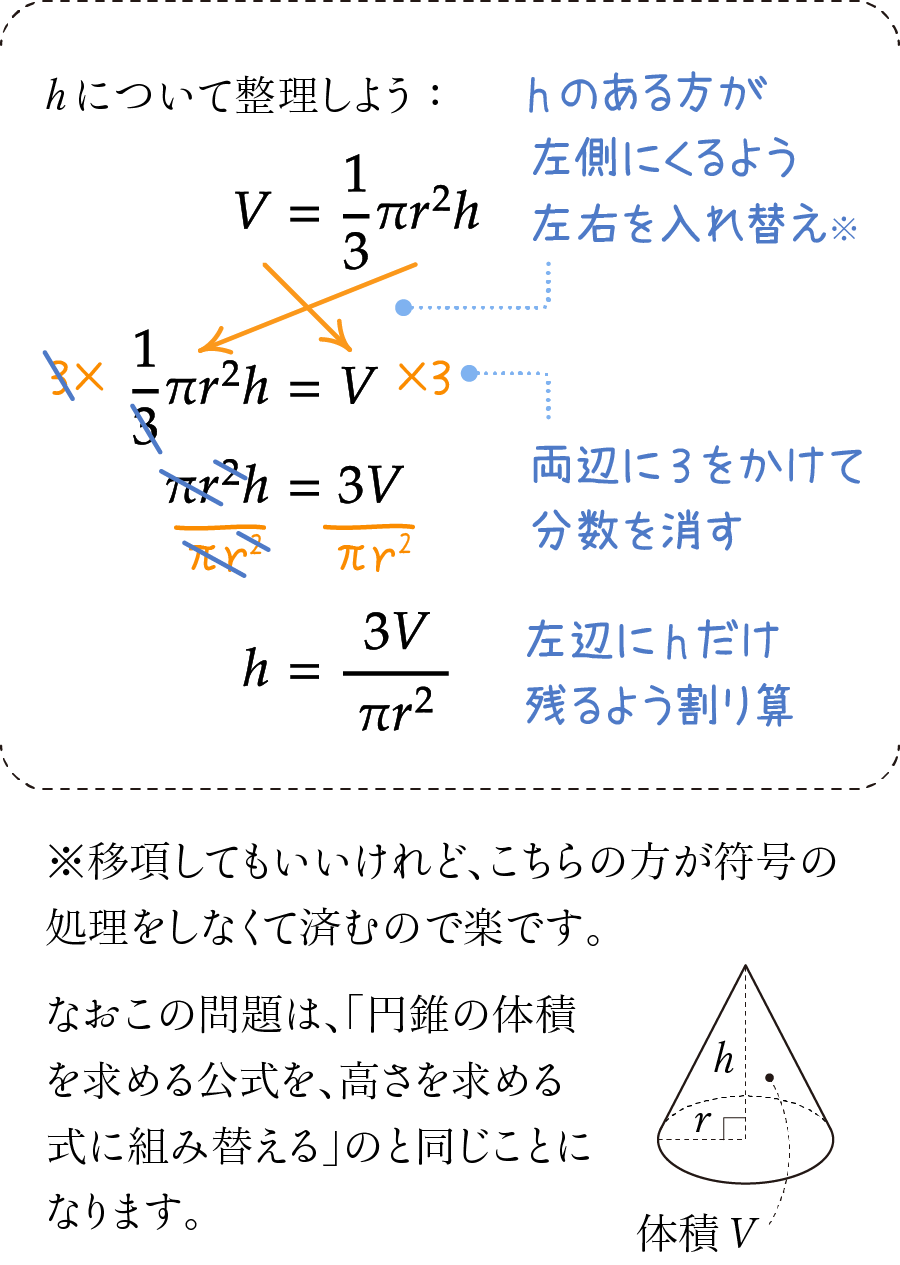
【例題3】 ちょっと複雑なパターン

式の中に分数やかっこが複数入ってくると、手順は多めになります。

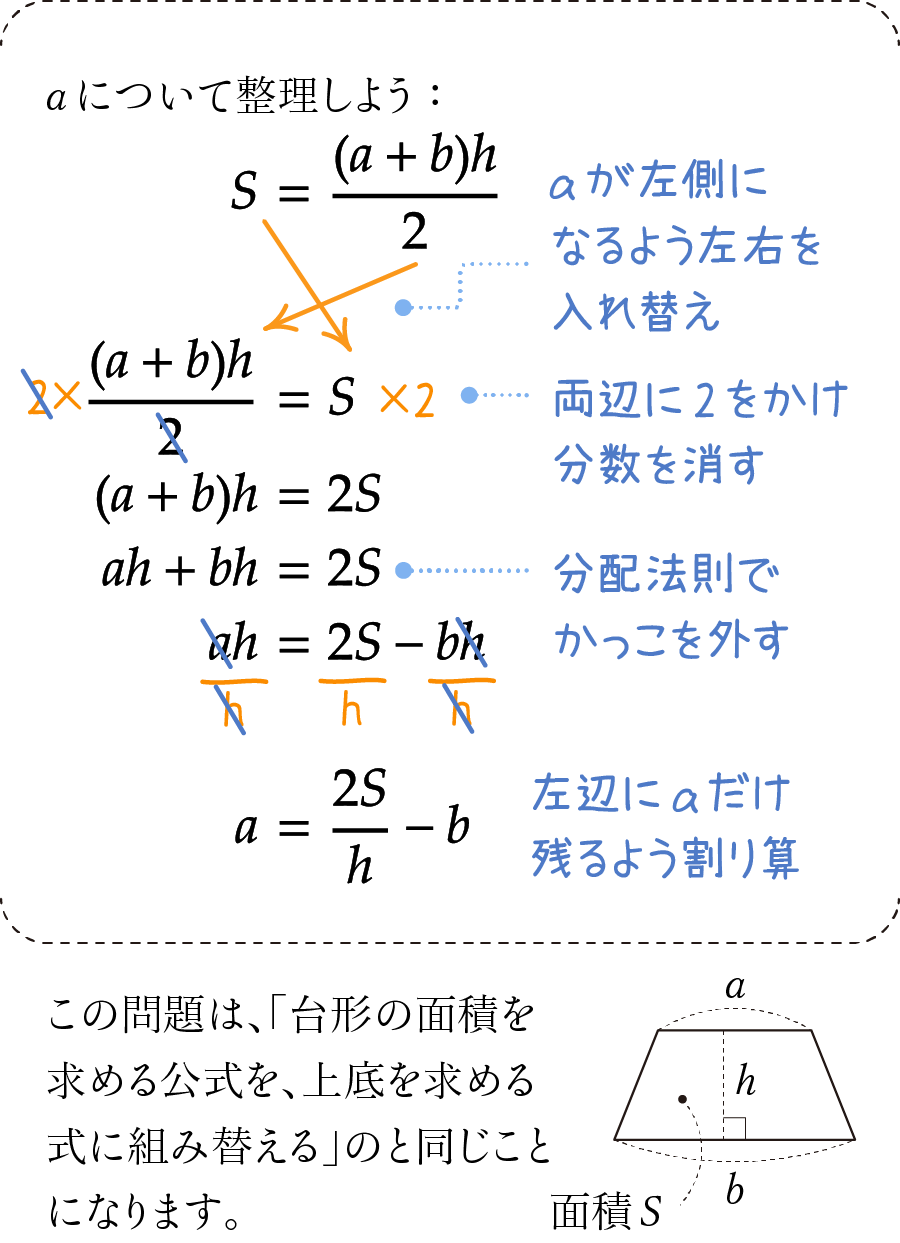
合計で6行という大がかりな計算となりましたが、こういう場合は複数の計算を一気にやろうとすると失敗してしまうので、このぐらいまで細分化した方がかえって速く片付きます。