1次関数がさっぱりという方へ、変化の割合と切片について基礎から確認

中学2年生の関数分野ですが、この分野が苦手な方は、まず式の中に現れる「変化の割合」と「切片」のイメージをつかむところから初めてみましょう。ここでは教科書的な説明は避けて、頭の中でイメージを描きやすいように図表で解説してみたいと思います。

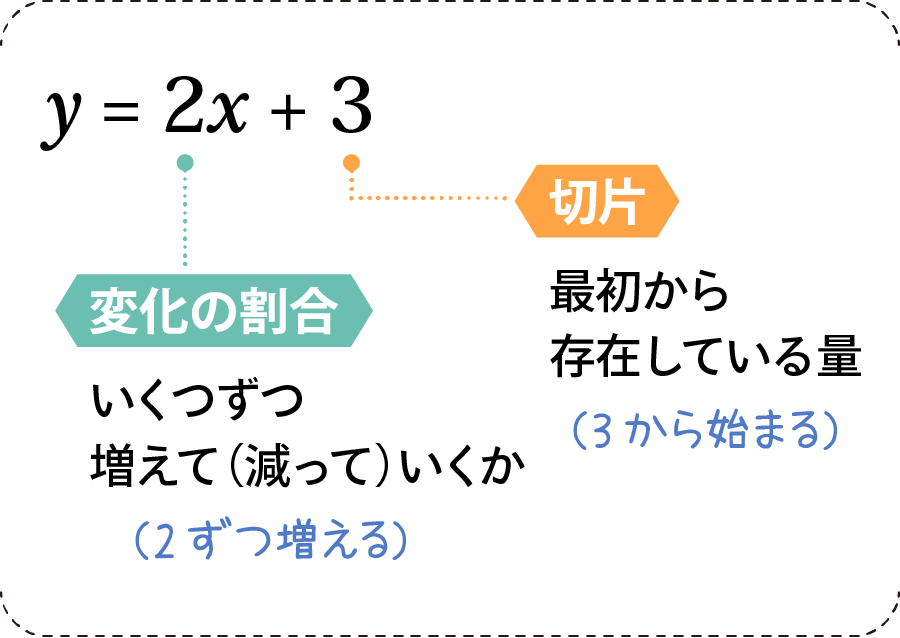
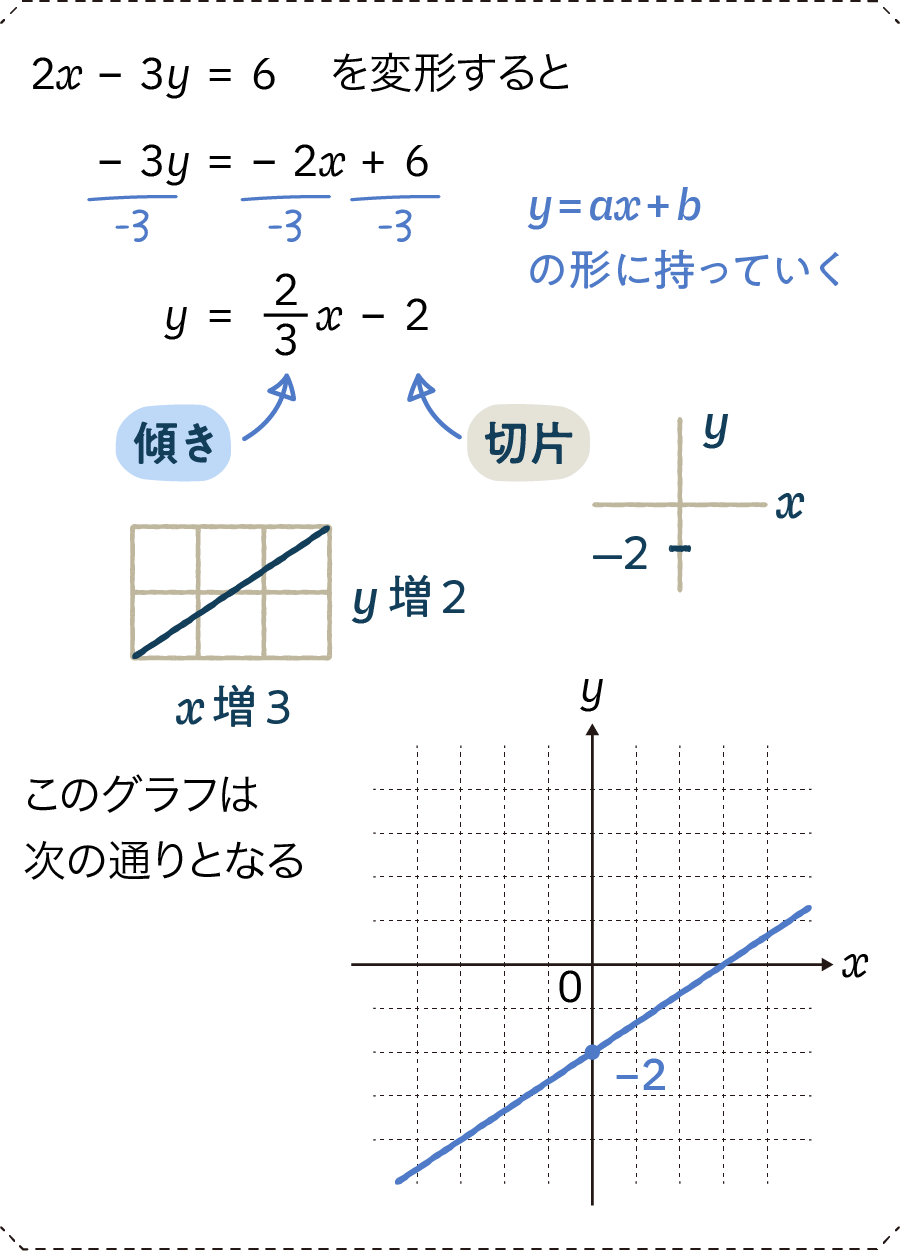
1次関数はy=ax+bという式で表せますが、aに当たる部分が変化の割合、bが切片です。bをスタート地点として（※）、aずつ数値が増えて（減って）いくというイメージです。

※関数はプラス方向だけでなく、マイナス方向にも伸びていくので、「スタート地点」というのは正確な言い方ではないのですが、とりあえずこうイメージしておくと理解が早まります。

一次関数の式で表せる典型的な場面をいくつか見てみましょう。

いずれの場合も、最初にあった量が一定割合で増減するというイメージですね。変化の割合は「変化のスピード」と考えてよいかもしれません。

表にしてみると

一次関数の式を表にしてみると下のようになります。y=2x+3という式であれば、yの値は「3から始まり、2ずつ増える」ということがはっきりわかると思います。

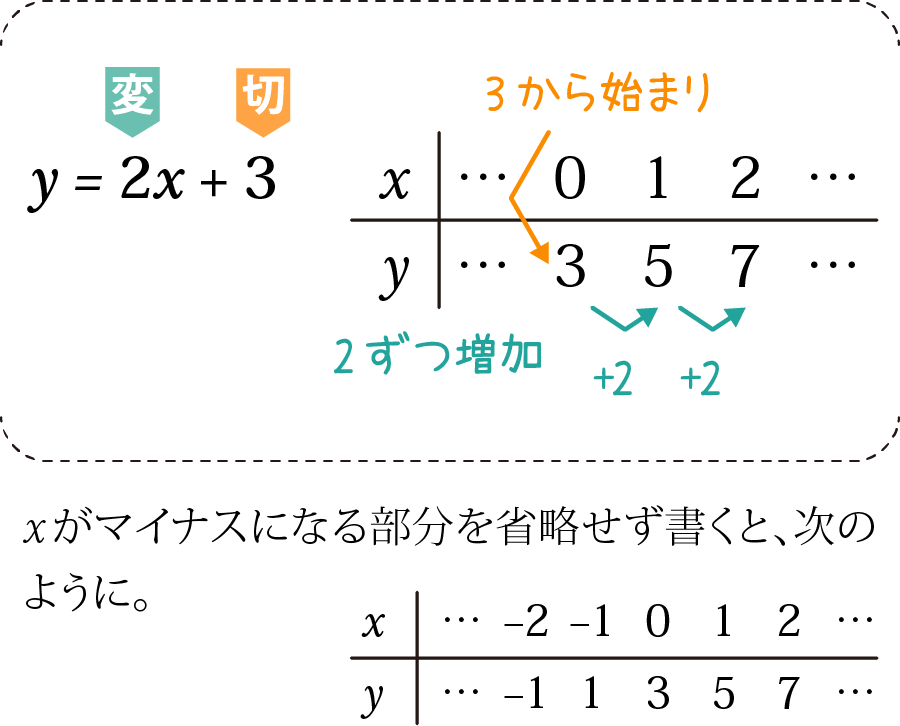
ここまで「切片3」を「3から始まる」と表現してきました。繰り返しになりますが、xはマイナスの数値にもなりうるので、そこを考えると本当は「3からスタート」というのは不正確です。切片をきちんと説明しようとすれば、「x=0のときのyの値」という表現になるでしょうか。

表ときたら、次はグラフで表してみましょう。切片はグラフのy軸上に存在し、この点を取るところから書き始めます。

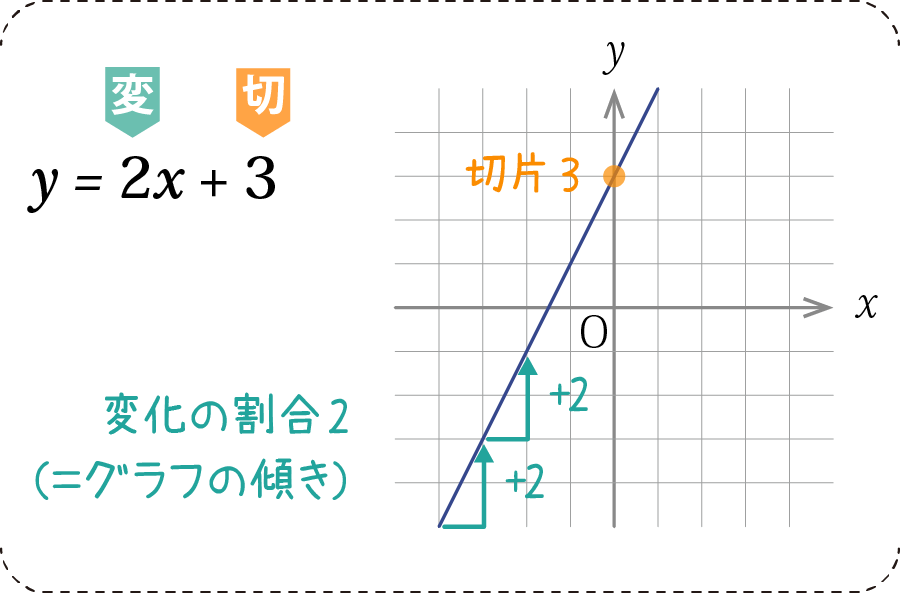
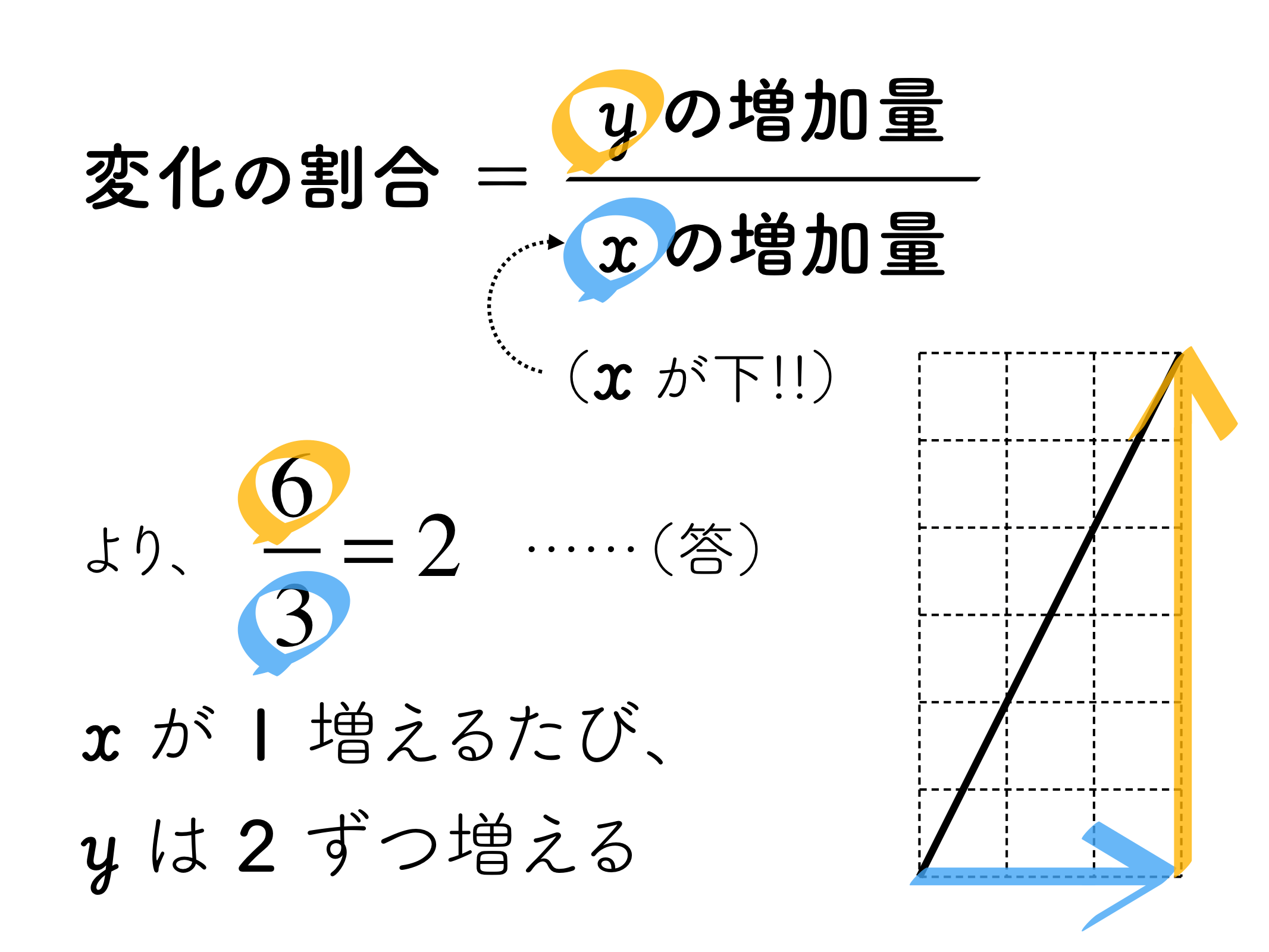
また、変化の割合はグラフの「傾き」となります。今回は傾きが2で、yは2ずつ増えていきます。もう少し正確に言うと「xが1増加する（右1マス進む）ごとに、yは2つ分増える」となります。

別の見方をすると、このグラフは「比例のグラフy=2xを、切片の分（上に3つ分）だけ押し上げた（平行移動させた）グラフ」という説明をすることもできます。

グラフを書く問題では、傾きに十分気をつけましょう。特に、グラフが右上がり（傾きプラス）なのか右下がり（傾きマイナス）なのかは真っ先に検討して欲しいところです。

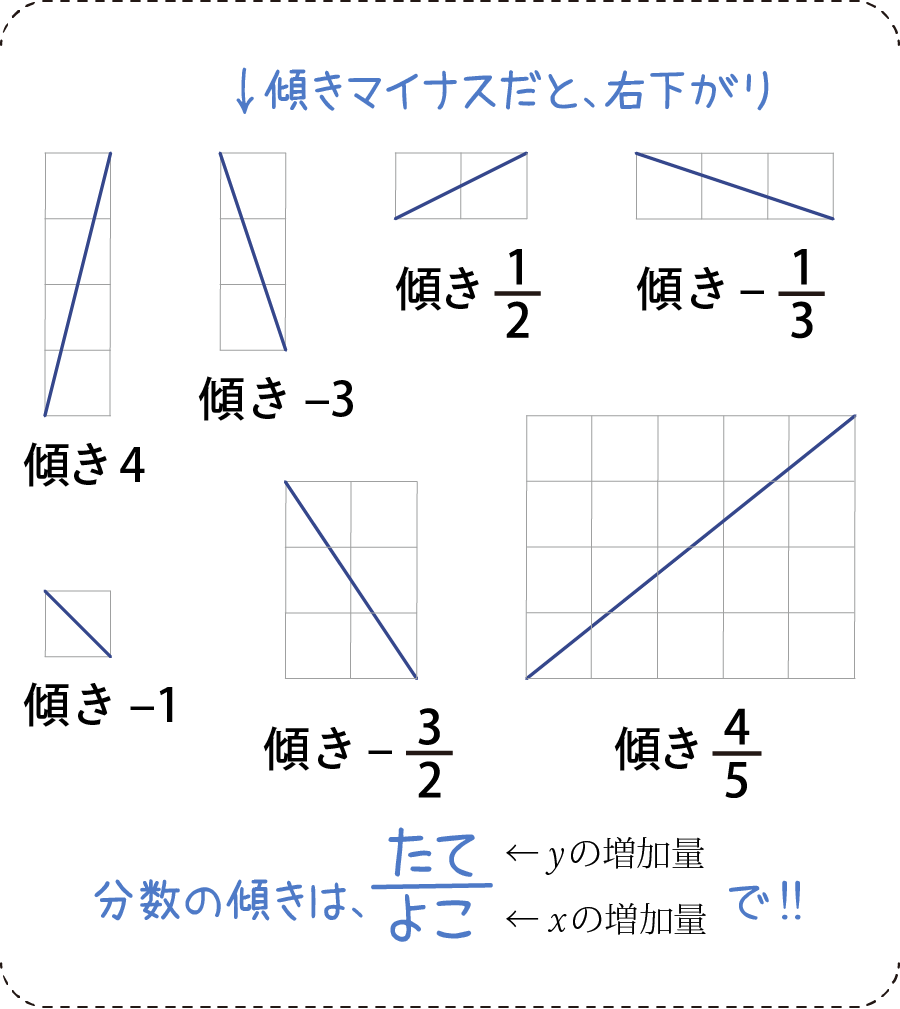
傾きが分数になるときの考え方も載せておきました。傾き4/5ときたら、xが5増える（右5マス）間にyは4増える（上4マス）という発想になります。

この考え方は、変化の割合を計算するとき重要になります。変化の割合を求める問題のページも大分前に作りましたが、やや舌足らずなのでそのうちリニューアルしたいと思います。