【中学数学】比例と反比例の性質を図表化する
比例・反比例のような「関数」の問題は、小学6年から中学1年にかけて結構力を入れて学習するところなのですが、反比例の問題を解くときに比例の計算をしてバツをもらったり、「どっちのやり方だっけ?」と迷ったりした経験はないでしょうか?
ここの分野は、まず比例の学習が終わったら比例の問題をひたすら解き、次に反比例を一通り習ったら反比例だけの問題ばっかりを……というようなやり方になることが多くて、少し時間が経ったら見事に知識がゴチャゴチャに、ということが起こりやすいです。
そこで、今回は比例と反比例の性質を見比べる図表を作ってみました。この2つを表やグラフにした時のイメージがきちんとできるようになれば、多少難しい文章問題でも解きやすくなると思います。それではいってみましょう!
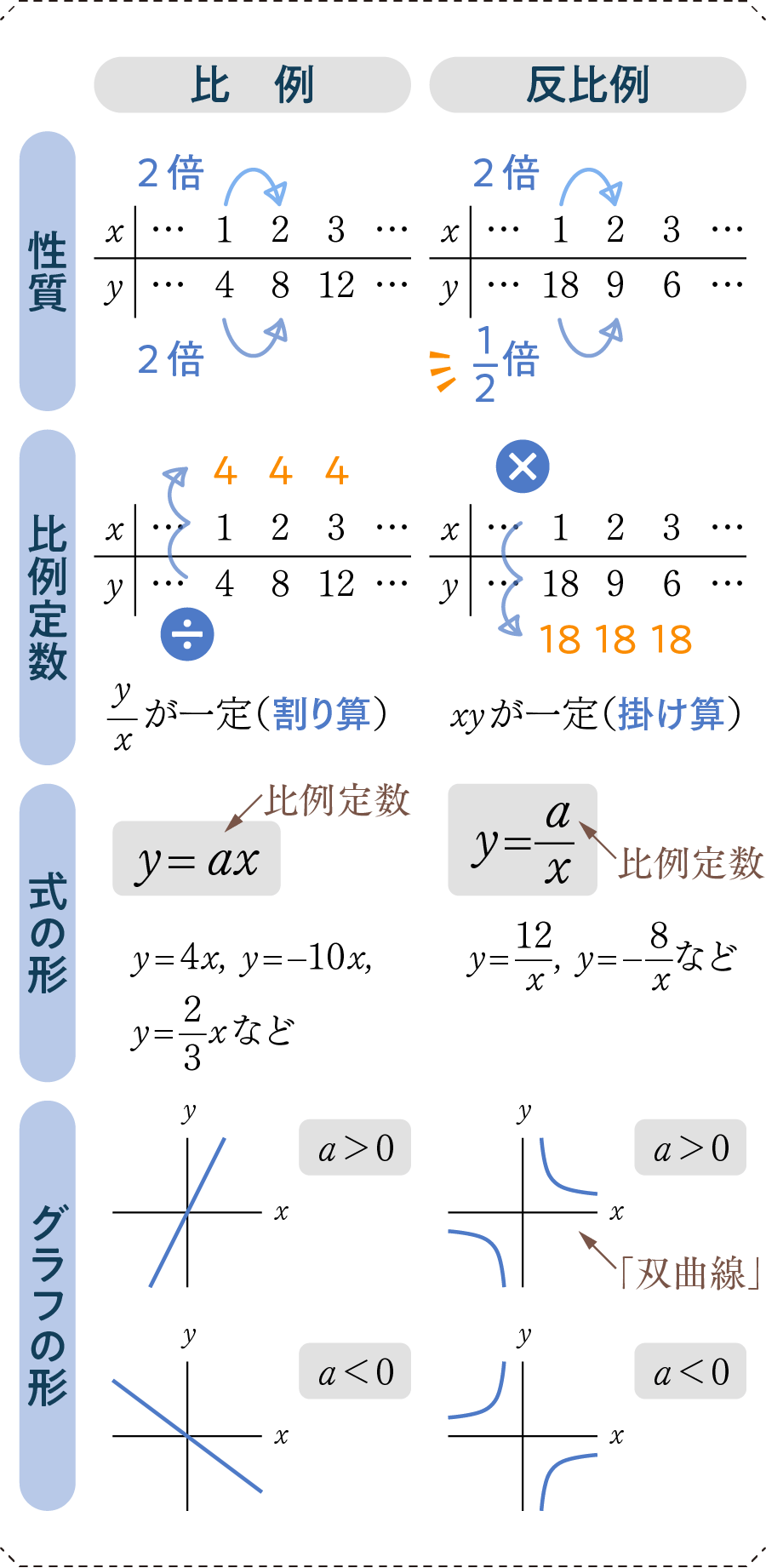
図表に書いてあることをまとめると、
- xを2倍、3倍……としたとき、yも2倍、3倍……となるのが比例。反比例は、2分の1、3分の1と変化していく
- 比例ではy÷xの値が一定。反比例はx×yの値がつねに一定
- 反比例の式はxが必ず分母に来る
- 比例のグラフは直線。反比例のグラフは「双曲線」
となります。
式の求め方(教科書的なやり方)
ここで、xとyを式に代入して、比例・反比例の式を求める計算について見てみたいと思います。まずは比例から。
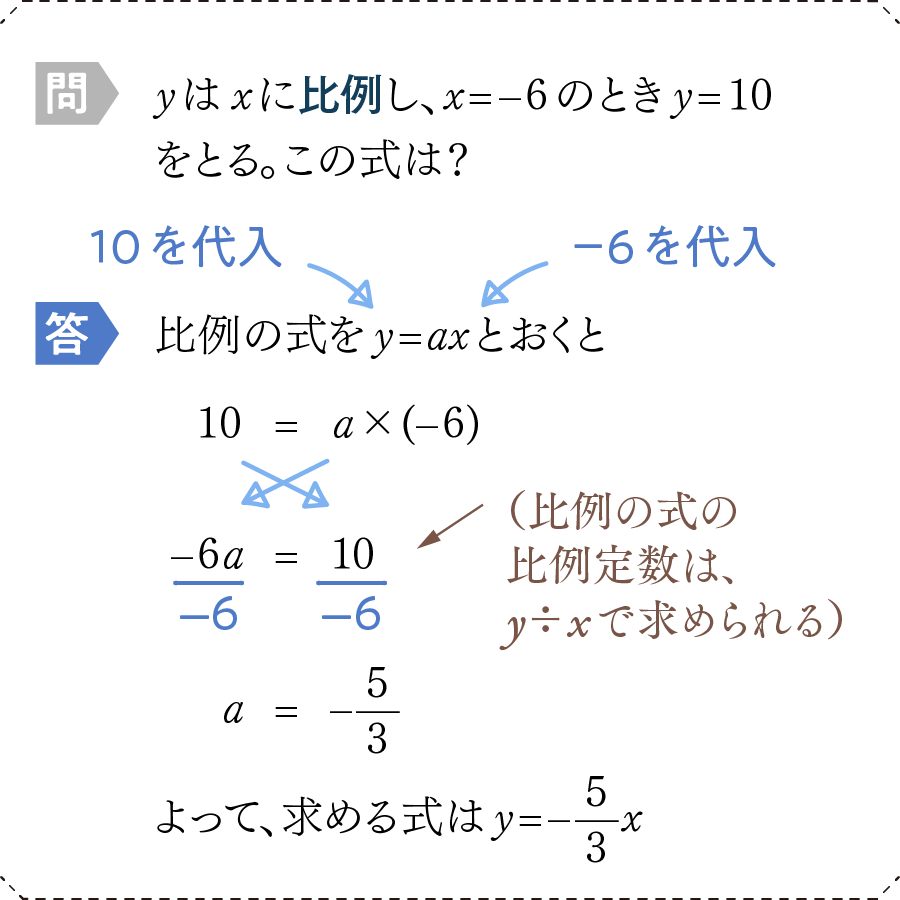
比例の式y=axに、xとyの値を入れていきます。すると文字がaだけ残りますので、一次方程式の要領でaの解を求めればOKです。aの値が出てきたら、元の式に判明したaの値を入れてやると答えになります。
上の例は教科書的な解き方ですが、比例定数はy÷xで求められます(一番最初の図表にも書いてあるよ!)ので、これを覚えていれば「10÷6=-5/3だから……」といった具合にすぐ答えが出せます。慣れてきたらこのやり方がいいと思います。
次に反比例です。
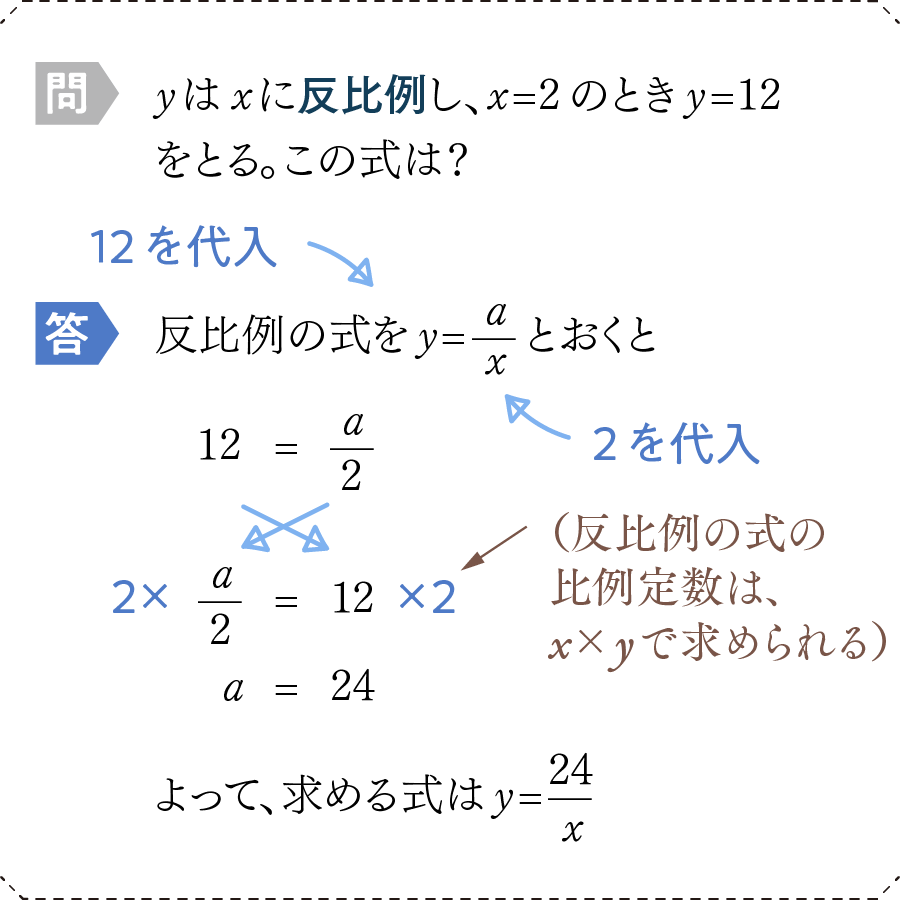
反比例は分数の式ですから、ちょっと面倒な計算ですね。反比例の場合、比例定数(なぜか「反比例定数」とは言わないのです)はx×yで簡単に求められるので、それさえ知っていれば近道できます。