中1の分数計算、ここに注意
数学の計算で分数が出てくると、手順が多くて面倒だなと感じる方が多いと思います。中1の分数計算では、似たような問題で微妙に違う解き方をするものがありますので、このページでご紹介します。もし小学校の分数計算があやふやでしたら、小学校の復習用のページ(前編・後編)もありますのでご覧ください。
話を元に戻して、文字式を使う次の2つの計算では分数の扱いがちょっとだけ異なるのですが、手順を思い出せるでしょうか?
- 「次の計算をしなさい(簡単にしなさい)」
→式を整理してシンプルな形にまとめる問題 - 「次の一次方程式を解きなさい」
→xの中身を求める問題
具体例がないとイメージしにくいと思うので、図表をご用意しました。
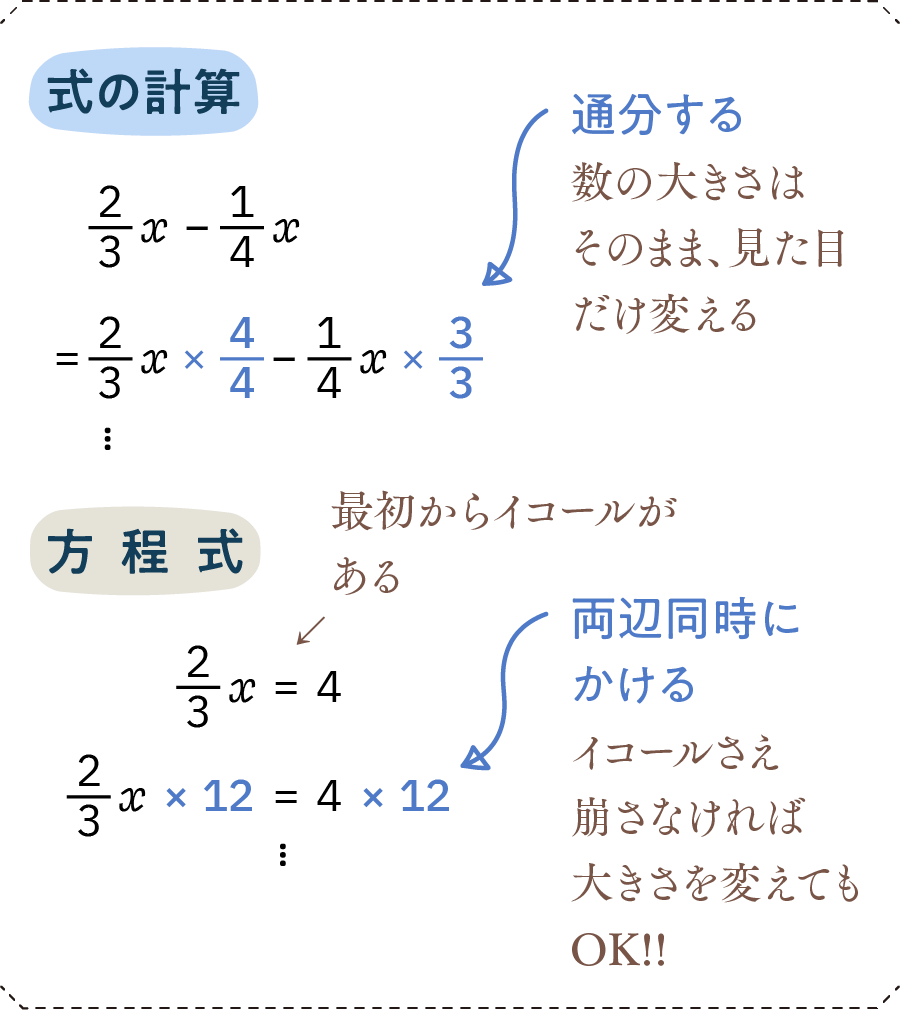
上の例、「計算しなさい」という問題では、通分を使って計算を進めていきます。通分すると数字の見た目は変わるのですが、数字の大きさ自体は変わりません(例えば「4分の4」をかけるというのは「1をかける」ことと同じですので、当然と言ったら当然ですが)。
一方で下のように方程式を解く場合は、「全体に数字をかけて、分数を消去してしまう」というやり方ができます。方程式を解く場合、イコールの関係を崩さなければ数字の大きさを自体を変えてしまってもOKなのです。
なお方程式の場合、通分して解くこともできますが、ちょっと効率の悪いやり方になってしまいます。
では、もうちょっと具体的な問題も見てみましょう。
問題その1
「計算しなさい」
まず、分数がズラズラと並んだ式をシンプルにする問題からです。
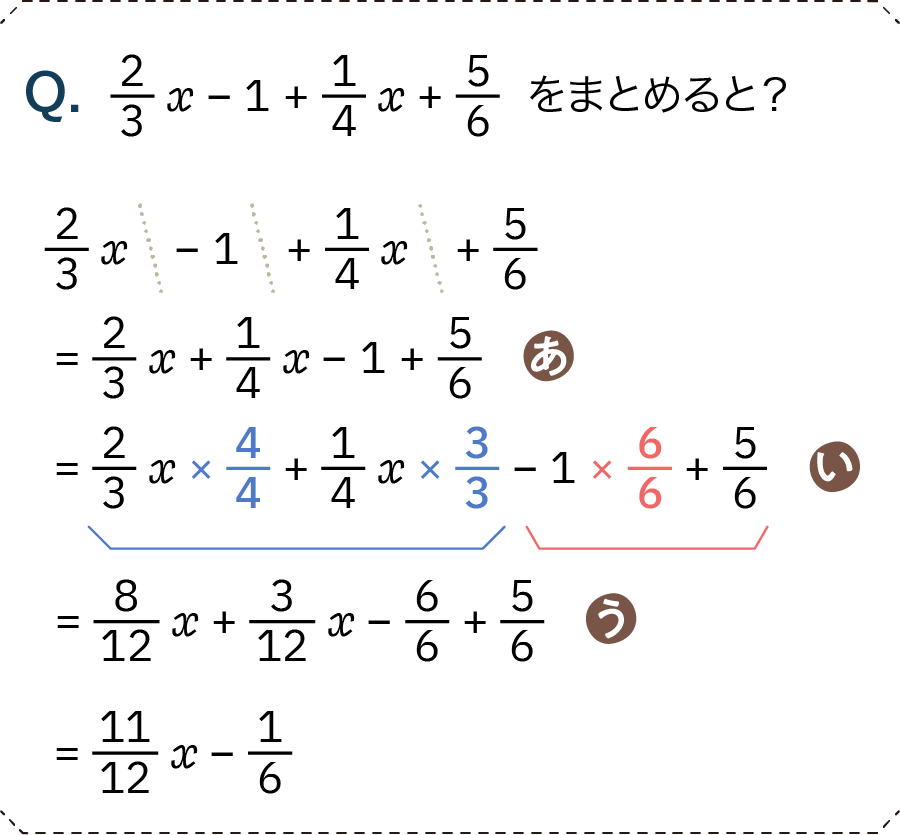
- あ……xのある項とない項に分類して、順序を変える
- この式は4つの項に分けることができます。符号の前のところで線を引いてみるとわかりやすいと思います
- い……それぞれのグループで通分する
- xのある項(青)は分母を12に、数字だけの項(赤)は6にします。
- う……分母が揃ったので、足し算でまとめて完成
方程式を「解きなさい」
次に、上の問題をちょっと組み替えて、1次方程式の問題にしてみます。
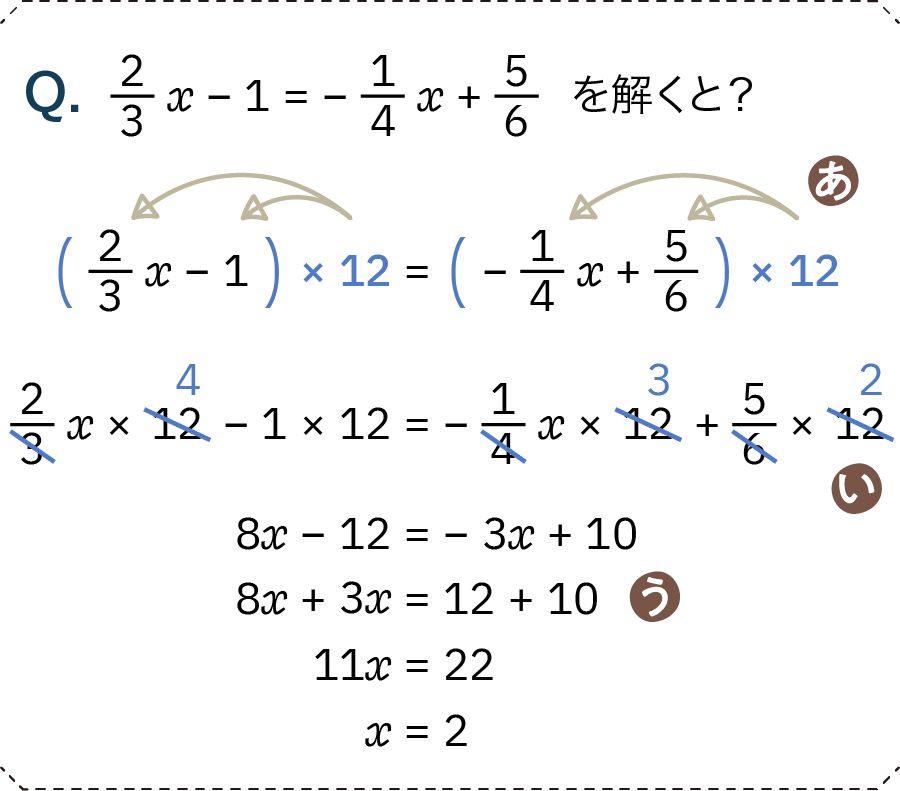
- あ……両辺に12をかける
- 分母にでてくる数字は3, 4, 6です。この3つの最小公倍数(つまり、3・4・6の段に出てくる九九の数字でなるべく小さいもの)は12ですので、全体に12をかけると一気に分数を消去できます
- い……分配法則でかけ算をする
- 慣れてきたら、「手順あ」を飛ばしていきなり「手順い」に言ってしまって構いません
- う……xのある項を左に、ない項を右に移行して答えに持っていく
問題その2
もう1つ、分数の問題をご覧ください。こちらは分子に複数の項があるパターン(横長の分数?)ですが、手順は一緒です。
「計算しなさい」
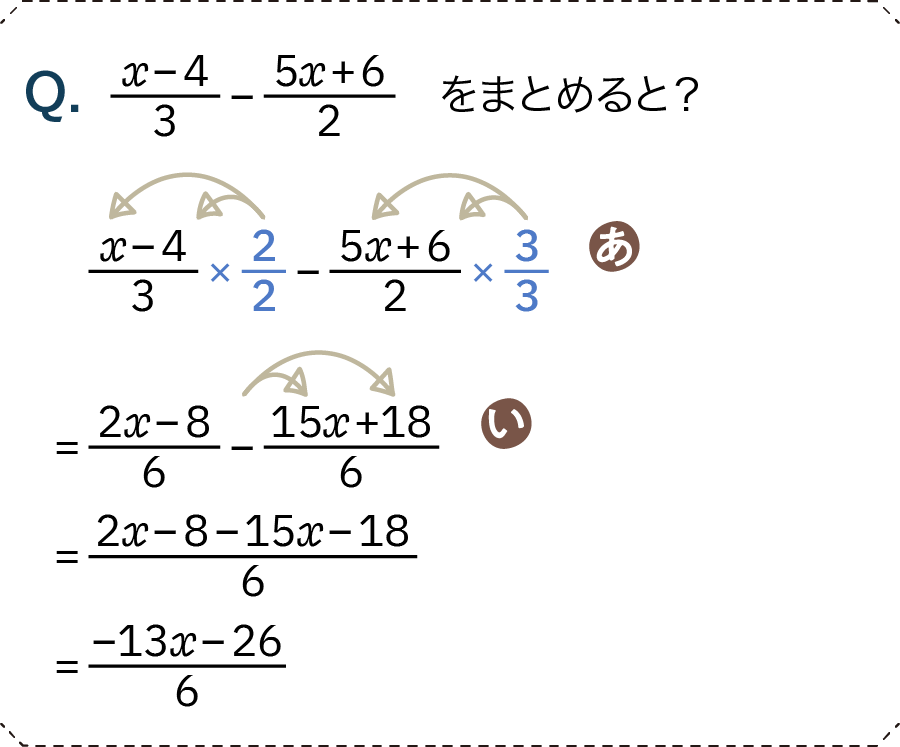
- あ……分母を6に揃えるため、通分する
- い……2つの分数を1つにまとめる
- 分数の前にマイナスが付いている場合、このマイナスはすべての項に影響しますので、分配法則で処理します(ここの部分、本当に計算ミスの多いところですのでご注意を!)
方程式を「解きなさい」
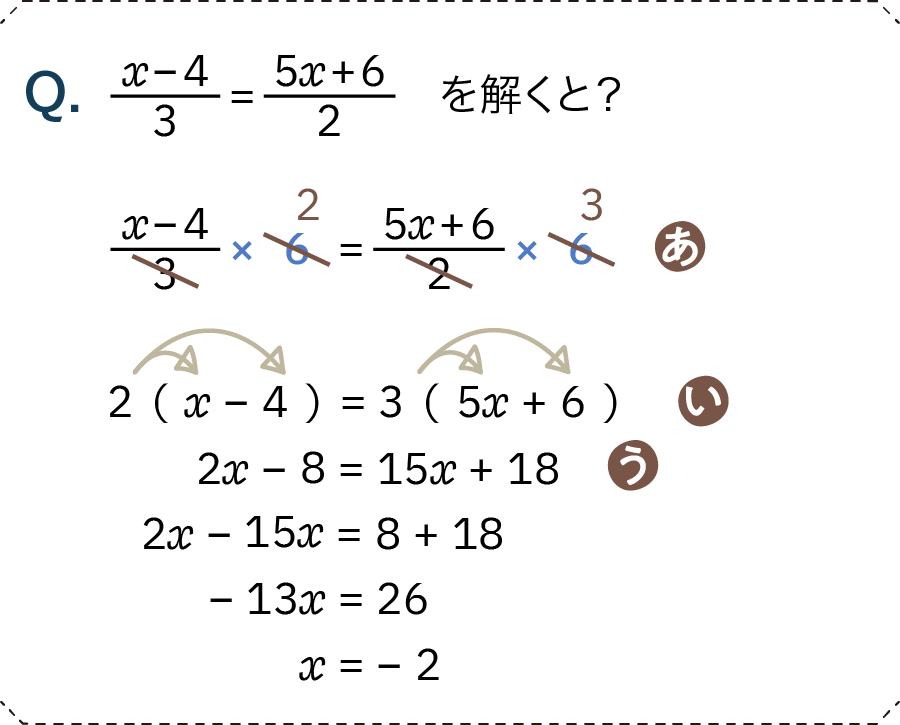
- あ……両辺に6(分母3と2の最小公倍数)をかける
- 分数の上に乗っかっていた部分がバラバラにならないよう、分数を消去した後はかっこを使ってまとめておきましょう
- い……分配法則でかっこを外す
- 慣れてきたら、「あ」の後でいきなり「う」の行へいっても大丈夫です
- う……あとはいつもの一次方程式と同じ手順です