2元1次方程式のグラフを書く2通りの方法

連立方程式の問題で出てきたような、「2x+y=5」や「8x-6y=24」という風に2つの文字が出てくる方程式について、グラフを書く問題の解説です。

名前の意味について一応確認してみると、文字が2つ登場するので「2元」、それぞれの項の中で文字同士がくっつかずに（かけ算にならずに）1つだけ単独で存在しているから「1次」という名前がついています。式の中に、もし「x²」とか「xy」のように、文字2つのかけ算の項が出てくれば「2次式」となります。

教科書にはやり方が2つ載っていて、1つは1次関数の定番である「y=ax+b」の形に式を変形していく方法になります。もう1つはxやyに0を代入することで座標を2つ探して点を取り、それを線で結ぶというやり方です。

【方法1】 y=ax+bの形にする

最初の方法として、式を1次関数の問題で見慣れた「y=ax+b」の形に変えていくやり方があります。中学2年の前半で習う「等式変形（～について解く）」と同じ手順で式変形していきます。

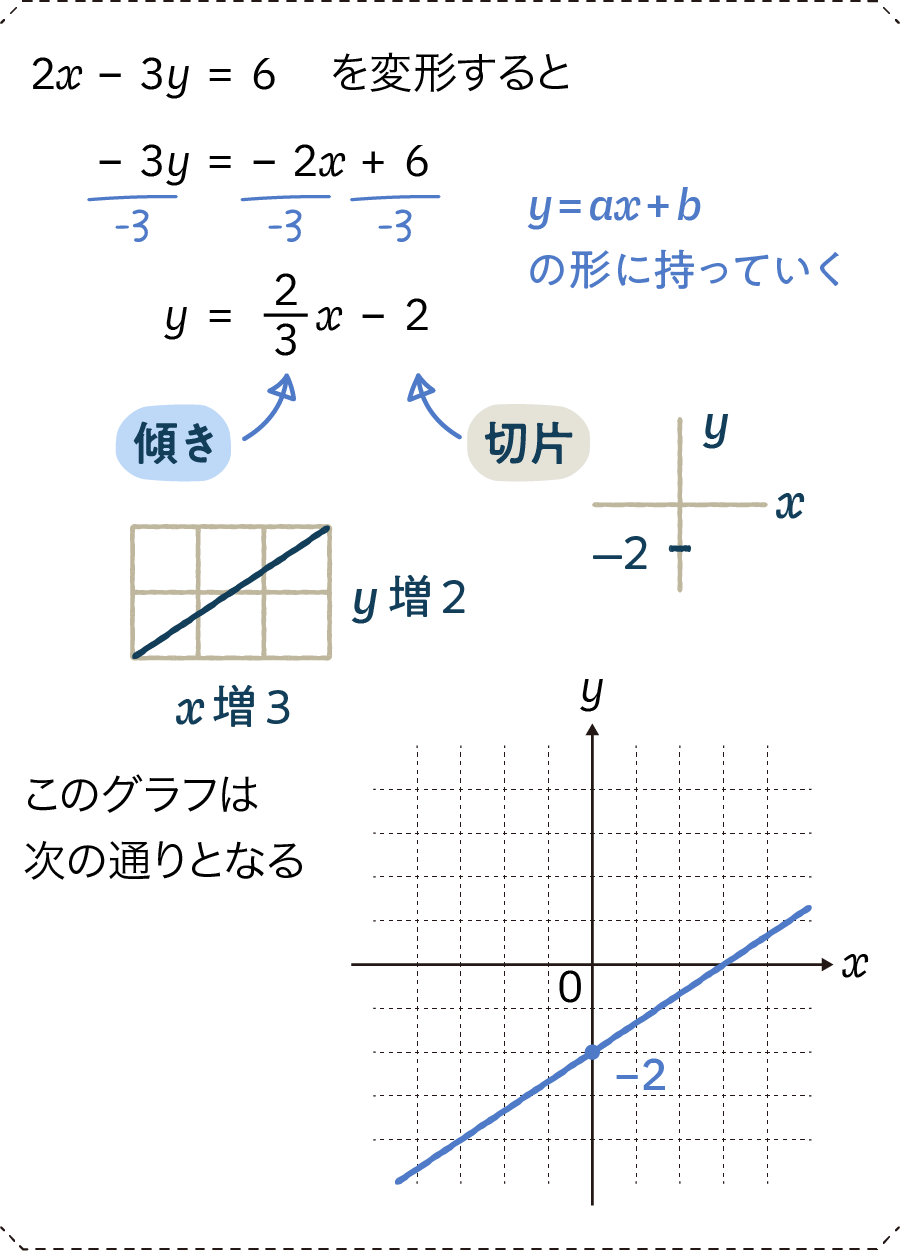
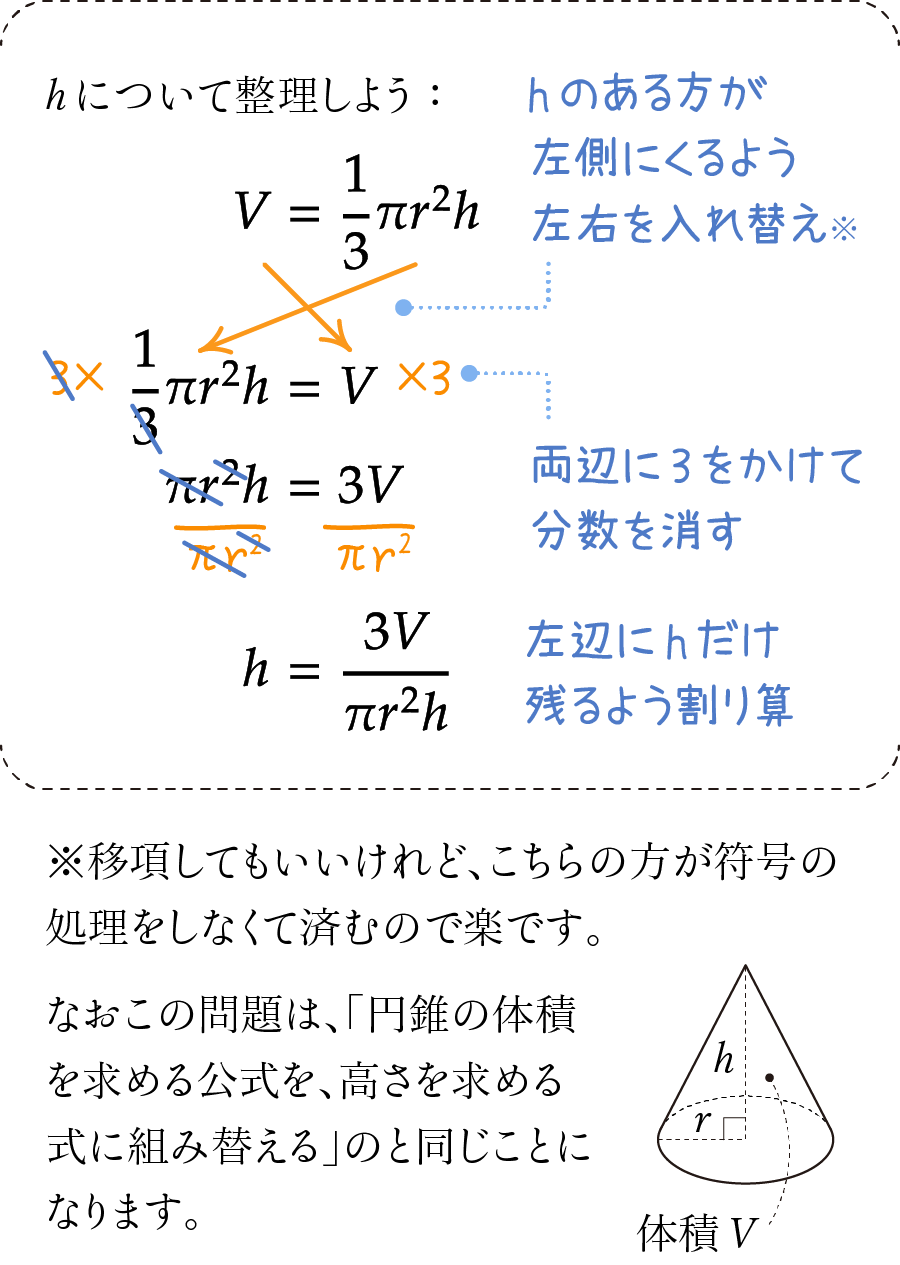
「y=」で始まる形にもっていくので、yのついた項以外をすべて右側に移動させます。あとはすべての項を割り算して左側にyだけ残るようにすれば、式変形は完成です。

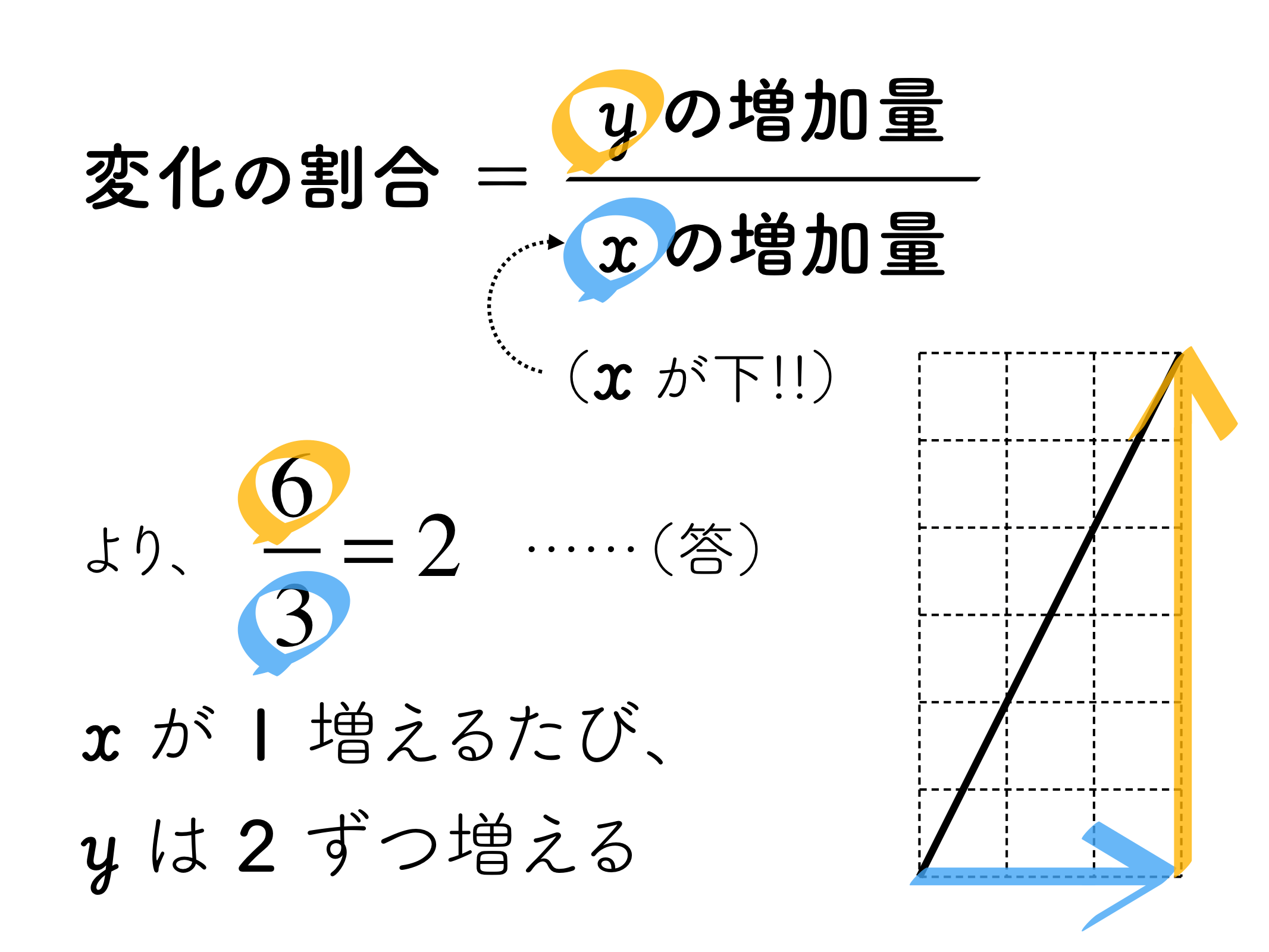
これでグラフを書く準備が整ったので、あとは式の「傾きと切片」を読み取って書いていきます。今回のように傾きが分数のときは、分母がxの増加量、分子がyの増加量となります。例えば傾き3分の2というのは、x方向（横）に3増えて、y方向（縦）に2増えるグラフをイメージすれば大丈夫です。

もう1つのやり方は、比較的計算しやすく、慣れた人なら数秒でグラフが書けるという方法です。まず元の式のxに0を代入してyの値を求め、つぎにyに0を代入してxの値を調べます。こうすると、グラフ上にある2点の座標が判明するので、この2つの点を線で結べば完成です。

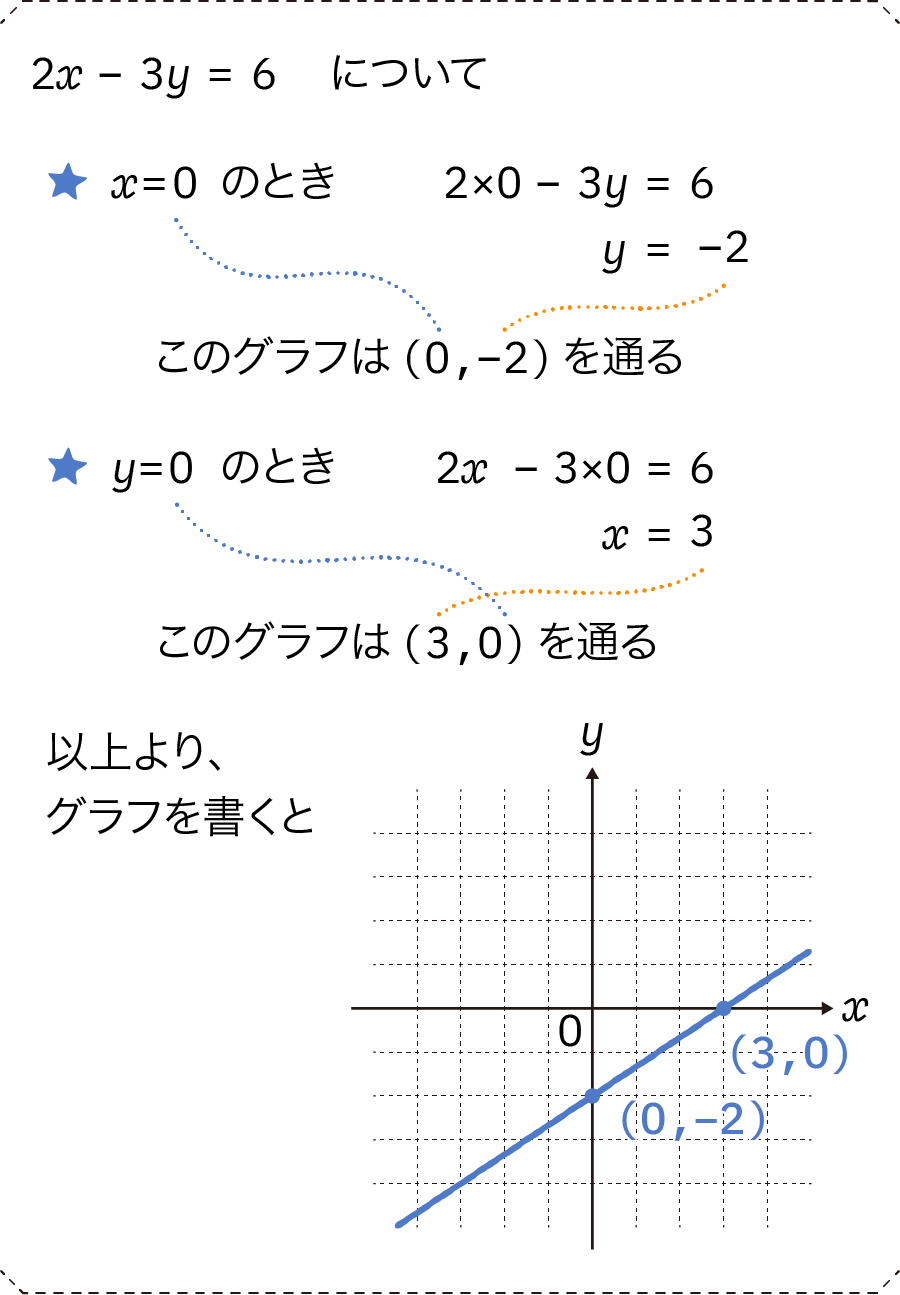
この方法は、式の右辺がxやyの係数を整数倍した形になっていればバッチリ上手くいきます。今回の式は「2x-3y=6」ですが、2と6は倍数の関係で、-3と6も倍数の関係になっていますので、計算してみると座標が整数できれいに出てきます。他には

のような式も大丈夫のはずです。

（このブログでは他にも1次関数についての記事を書いています。ページ下の「1次関数」のタグを押してみて下さい）