これで納得いく？解と係数の関係

数学II、2次方程式の解と係数の関係について確認です。公式はとてもシンプルなのですが、その分記憶から抜け落ちるのも速いので、理屈をふまえて図解してみようと思います。

図解でご説明

実はこの「解と係数の関係」の公式は、中学校で学習した展開公式（4つあるうちの最初のもの）と考え方が同じなのです。図をご覧ください。

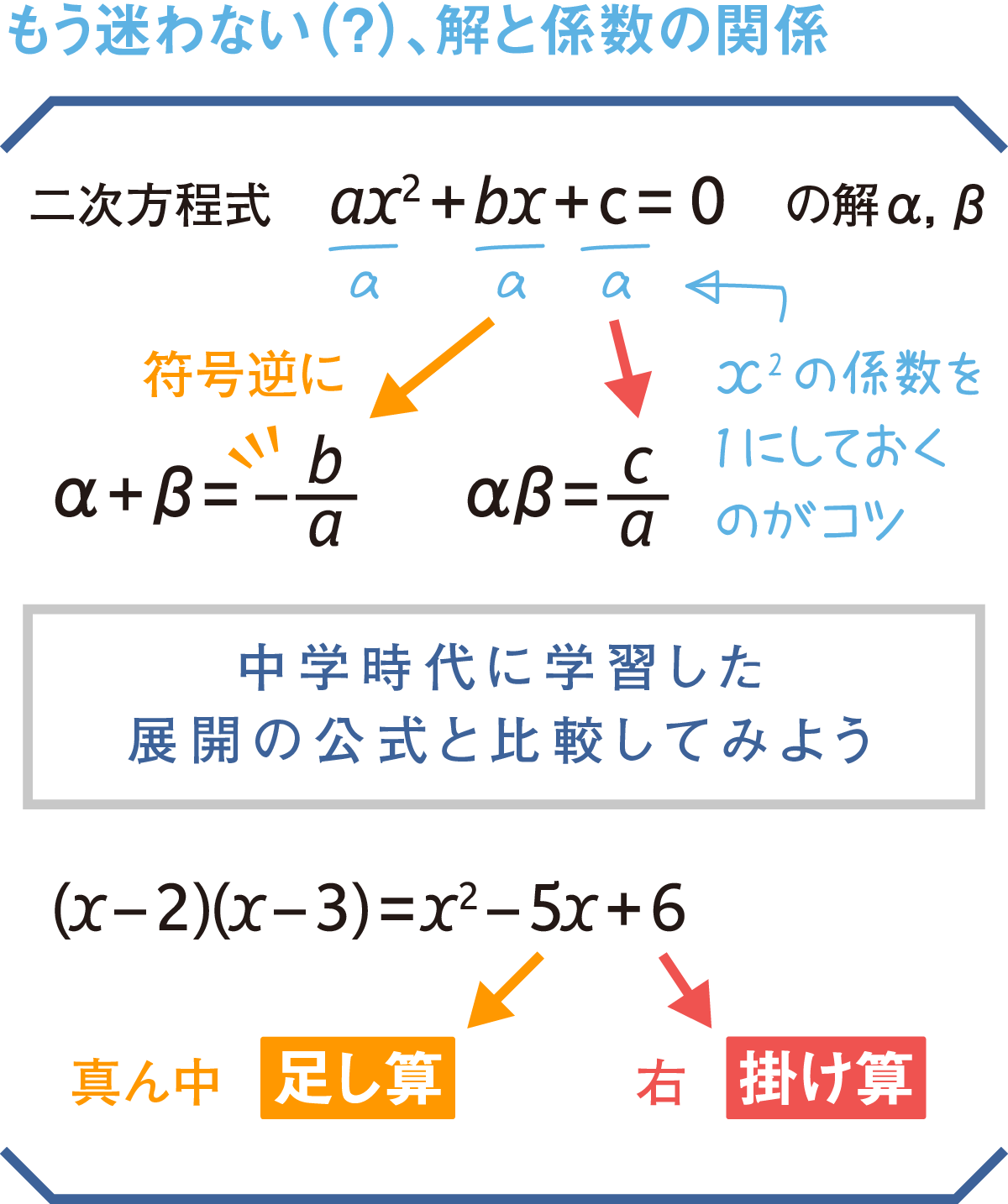
展開公式と一緒に並べてみると、解と係数の公式の意味が何となく見えてくると思います。方程式全体をaで割り（※）、x²の係数を1にしておくところにもご注目。これで公式がだいぶ扱いやすくなると思います。

※今回は2次方程式ですから、aは0ではないことが前提です。数をゼロで割ることはできないので念のため。

実際に計算してみよう

それでは、2次方程式の解の和（α+β）と積（αβ）を、実際の式に基づいて計算してみましょう。展開公式と同様に「真ん中の項は足し算、右端の項は掛け算」というのを念頭に置くとOK。

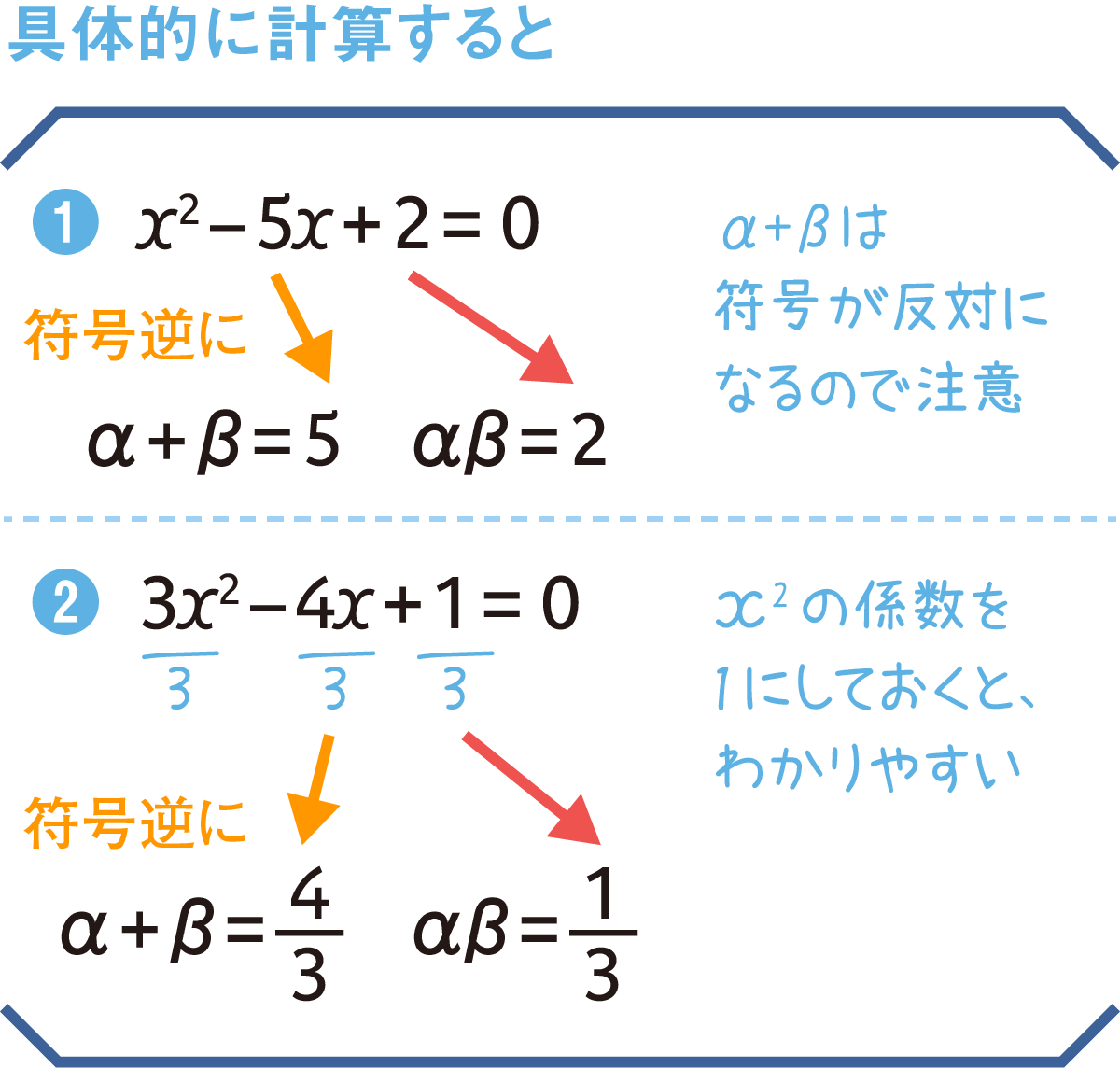
図では省略しましたが、記述式のときは「2次方程式～の2つの解をα, βとする」という一言を必ず添えておかないといけません。

補足・解の和がマイナスになる仕組み

解の和（α+β）を求めるとき、真ん中の項のプラスマイナスをひっくり返すわけですが、この仕組みについて、具体例と合わせて見てみたいと思います。

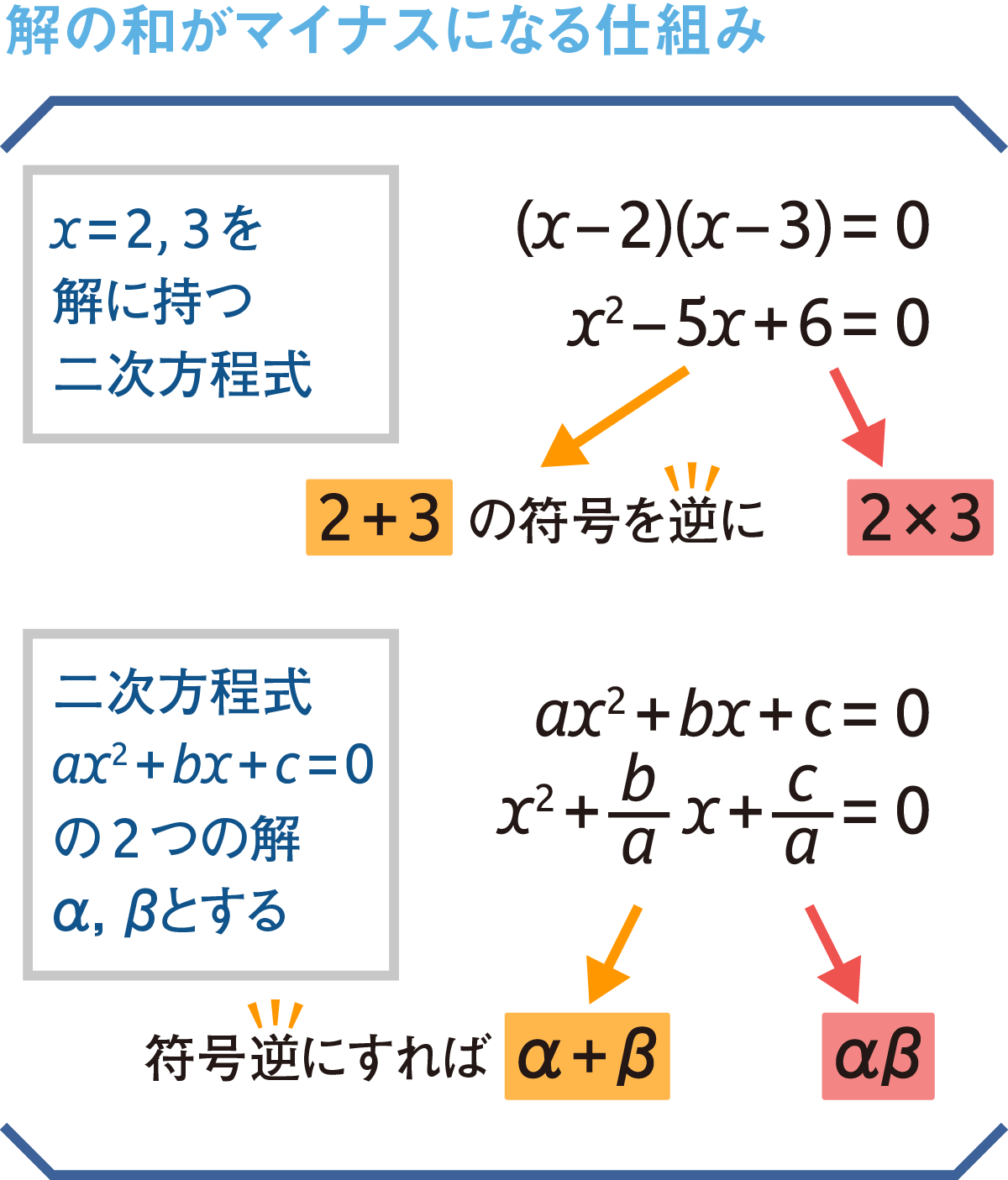
ご納得いただけましたか？このように、2次方程式の因数分解形を並べてみると分かりやすいと思います。