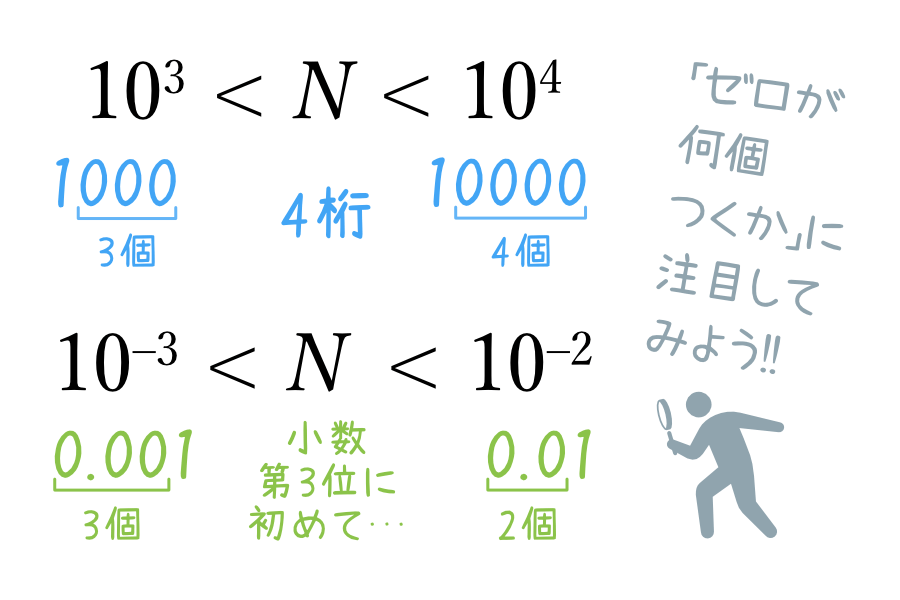
最大公約数・最小公倍数の公式(l=ga’b’やab=gl)のイメージを確認しよう

高校数学Aの整数分野で、最大公約数・最小公倍数について取り扱います。本格的に学習するのは小学校以来なわけですが、整数という数は意外に扱いにくい！ということを思い知らされるかもしれません。頑張っていきましょう！

まずは、英語での名称とそれぞれの考え方について簡単に確認。いちいち「最大公約数」「最小公倍数」と記述するのは面倒なため、アルファベットの略称を使うことがよくあります。

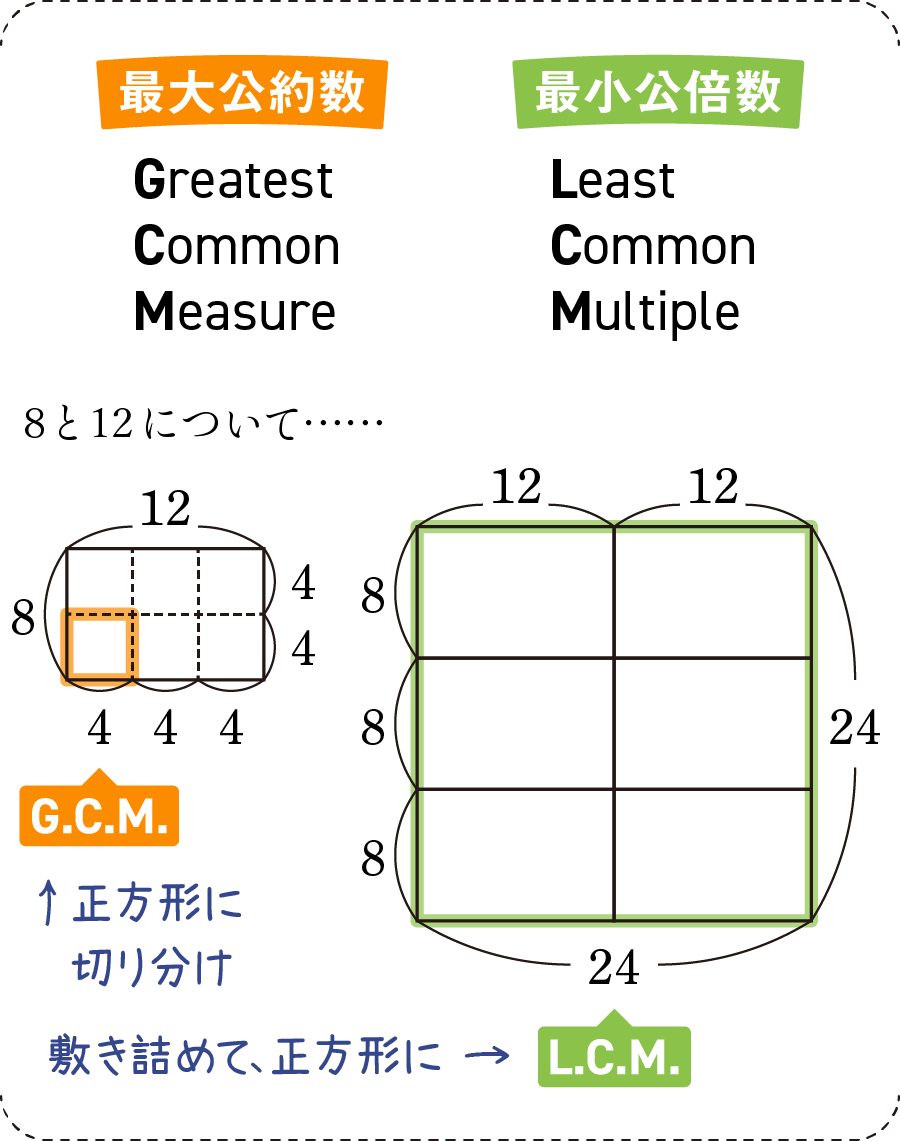
言葉の正確な定義は教科書等を見ていただくとして、例えば上の8と12であれば

という求め方になります。図形で考えると、8cm×12cmの長方形について

と想像するとよいでしょう（今回は取り上げませんが、「正方形で切り分ける」という発想は、最大公約数を求める「ユークリッドの互除法」でも扱うやり方です）。

同時に割り算しながら、G.C.M.やL.C.M.を求める

まず、単純に「最大公約数を求めよ」のような問題が出題されたら、下の図のように割り算しながら求めましょう。

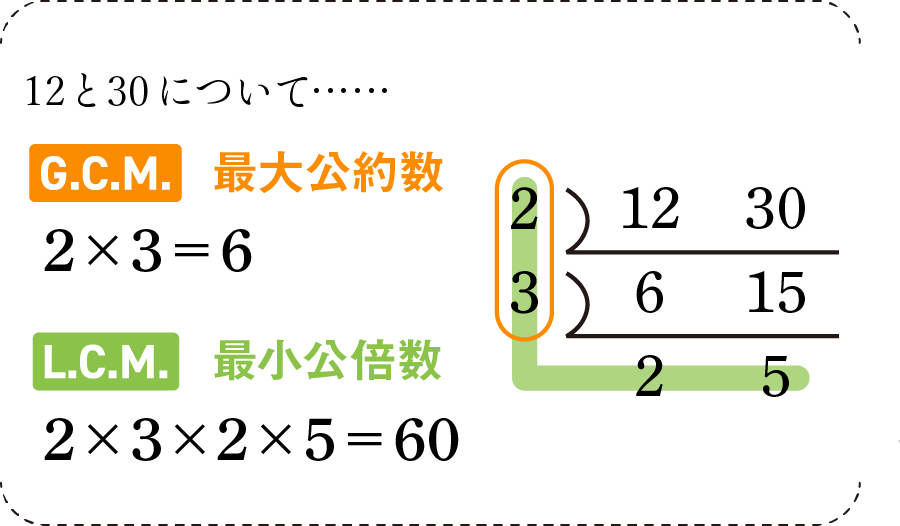
最大公約数は、両方とも割りきれる数を集めて、掛け算していくこととなります。一方で最小公倍数は、2つの数を掛け算にバラしたときの1個1個（因数）を全部集めていくと求めることができます。

最小公倍数は図の通り、L字型に掛け算しています。略称L.C.M.で、Lから始まることとセットで覚えると便利かも？

上と同じ計算を、素因数分解の形で書き表すと次のような感じになります（図を分かりやすくするため、累乗を使わずに表記しています）。

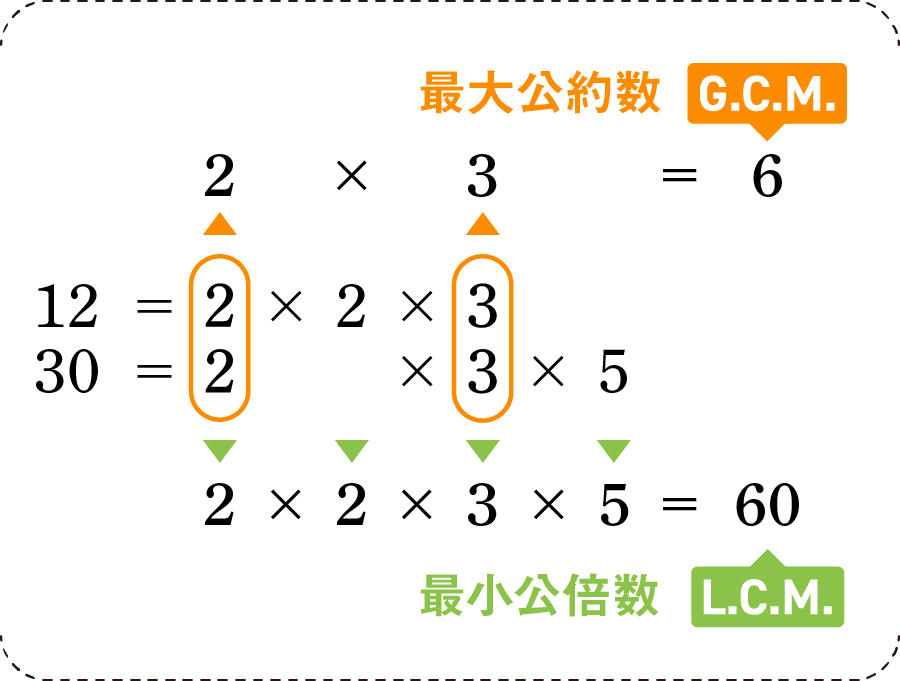
先ほどと同様、最大公約数は共通する因数を拾っていき、最小公倍数はすべての因数を掛け算すればOK。

ここから先が高校数学特有の話で、最大公約数・最小公倍数の関係を公式化したものを取り扱っていきます。

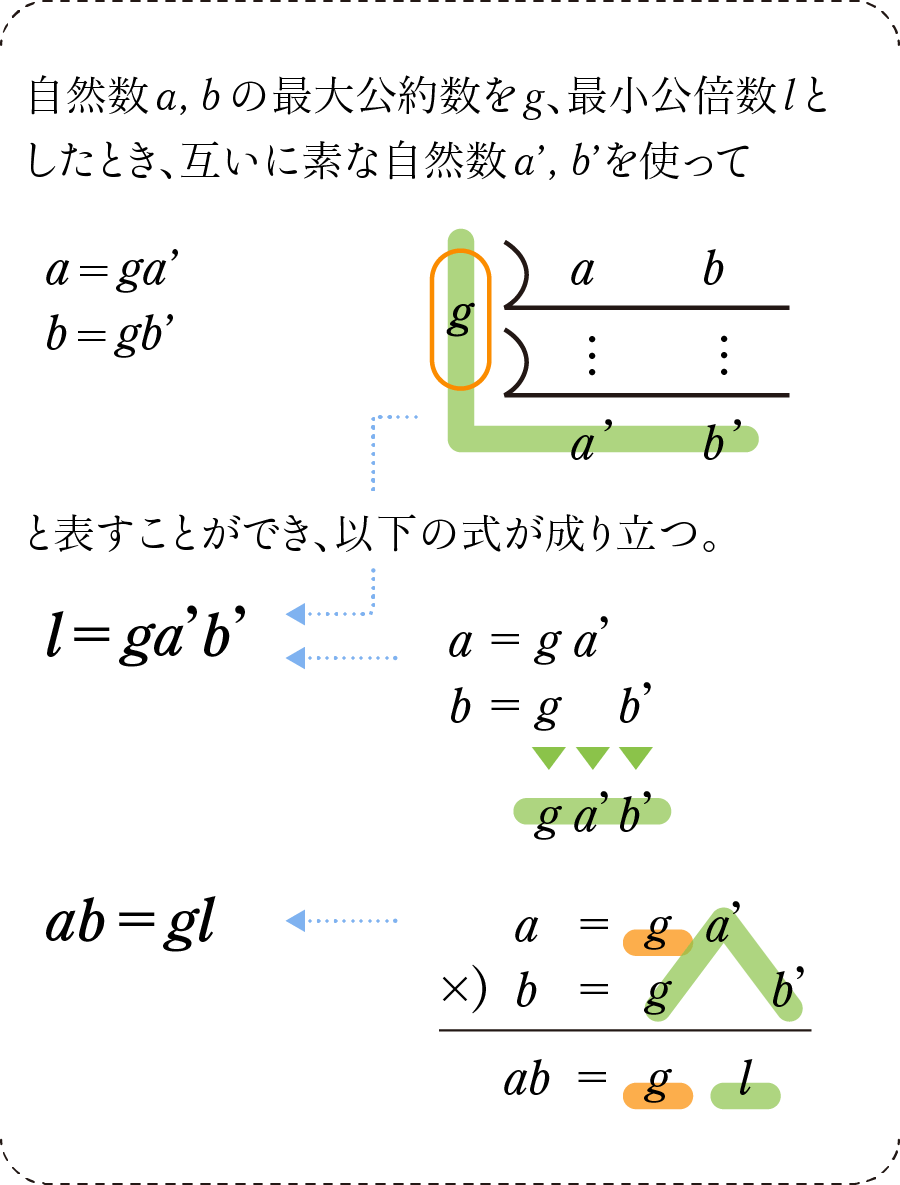
まず、元の数a, bに対してa’とb’というものが出てきますが、これは個人的に、果物をしぼってジュースにした後の「残りかす」のようなイメージで考えています。aとbを同時に割り算していくと公約数が取り出せますが、最後に残ったのがa’とb’です。

a’とb’はこれ以上公約数が（1以外に）取り出せない互いに素（※）な自然数となります。

※具体的に、4と7は1以外の整数で同時に割りきれないので互いに素といえます。一方で4と6は両方とも2で割れる（公約数に2を持つ）ため、互いに素ではありません。

話を戻して、最初の公式（l=ga’b’）は最小公倍数lについてのものですが、lだけに「L字型に掛け算する」ことを思い出せばOKです。

2つめの公式（ab=gl）は、暗記しやすい公式ではありますが、なぜそうなるかはなかなか説明しにくいところです。一応図を見てもらえばその理屈は分かるかと思います。