常用対数のケタ数問題、「どっちだったっけ？」と迷わないために

常用対数を使った問題といえば、桁数を求めたり、小数第何位にゼロ以外の数字が来るかを求める問題が定番です。でも、対数分野では他の問題に比べて出題率が高くないため、いざ出題されると「これって6桁だっけ？それとも7桁？」と迷ってしまう場面があると思うのです。

切り上げて考えればよい?!

そこで、答えに悩まずストレートにたどり着ける方法がないか、問題集を眺めて気づいたのが、桁数・小数首位いずれの問題も、「常用対数の値を求めたら小数を切り上げてしまえばいい」ということ。例えば、対数計算の結果が3.456だとしたら、切り上げて「4桁」と答えを出すわけです。そうすればマークシート問題で時間短縮できますし、記述式でも自信を持って答えが書けるかと思います。

対数計算がマイナスの場合も同じ取り扱い、つまり絶対値が大きくなるように数字を丸めます。つまり、-2.345だったら「小数第3位に……」という答えになりますし、-5.432だったら「小数第6位に……」と解答すればOKです。

ここで例題を2つほど見てみましょう。 \( \log_{10} 2 = 0.3010 \)としたとき、 \( 2^{20} \)の桁数を求めます。まず常用対数を計算すると

\begin{align*}
\log_{10}2^{20} &= 20 \log{10}_2 \\
&= 20 \times 0.3010 \\
&= 6.020
\end{align*}

この小数点部分を切り上げると7ですから、答えは7桁となります。

次に小数首位の問題、先ほどの数字を使って \( \left( \frac{1}{2} \right)^{30} \)の小数第何位にゼロ以外の数字が出てくるか求めてみましょう。

\begin{align*}
\log_{10}{\left( \frac{1}{2} \right)^{30}} &=
\log_{10}{2^{-20}} \\
&= -20 \log_{10}{2} \\
&= -20 \times 0.3010 \\
&= -9.030
\end{align*}

数字部分9.030について、小数を切り上げると10となるため、解答は「小数第10位に初めて0でない数字が現れる」です。

なお、常用対数の値がぴったり整数になるときは切り上げるというよりも1を足してしまえばOK。例えば100の常用対数は2であり、この時は1を足して3ケタの整数となるわけです。小数首位については、0.001の常用対数は-3のところ、3に1を足して4……といった要領です。

不等式で表した時のイメージ

記述式問題では今のように、「切り上げると7だからこの数字は7桁」などと書いてしまったら意味不明なことになります。そこで、\( 10^6<2^{20}<10^7 \)という具合で不等式で桁数を表すのがおなじみのパターンですが、イメージをはっきりさせるために図を作ってみました。

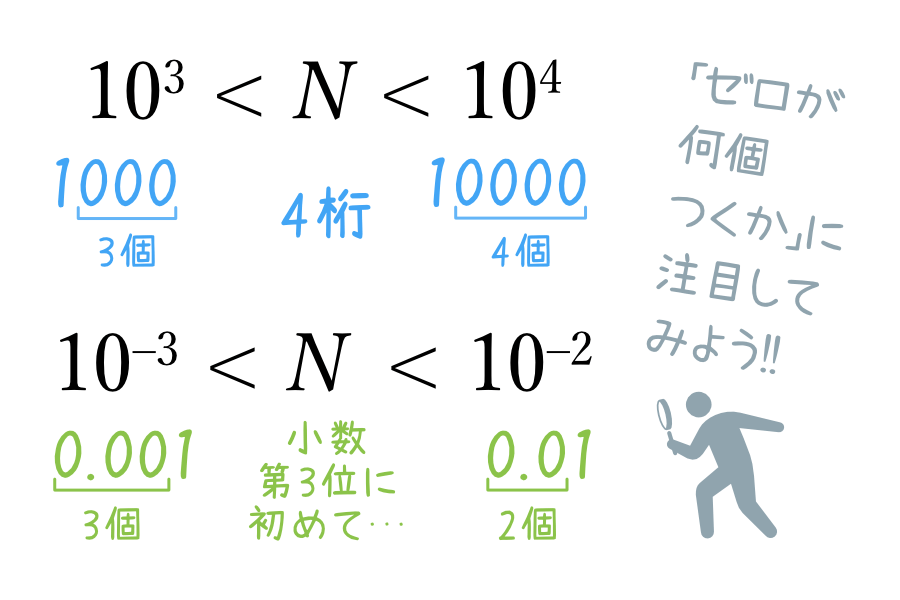
「10のn乗」ときたら、「0がn個つく」という考え方をすればOKです。