【アニメgif】なぜ10進数からn進数への変換で、割り算・かけ算を繰り返すの?
数学Aで学習するn進数の計算ですが、他の整数問題と違って単発の知識となりやすく、しばらく使わないでいるとすっかりやり方を忘れてしまいます。ここで計算方法の復習と、その手順の意味を確認してみましょう。
n進法はお金のイメージで?!
数字の位取りは、買い物の代金を支払うときのイメージで考えてみるとよいです。お会計の金額が231円とレジで出て来たら、まず財布から100円玉2枚、10円玉3枚、そして1円玉1枚を探すはずです(最近はキャッシュレスの流れで、小銭のやり取りの機会はかなり減りましたが)。
10進法はこのように10が位取りの基礎となりますが、例えば3進法なら3がベースのはずです。言ってみれば、1円玉、3円玉、9円玉、27円玉……でお支払いするようなイメージでしょうか。
これを図にすると次のようになります。ある数を0乗した場合、1になるということも押さえておくといいでしょう。
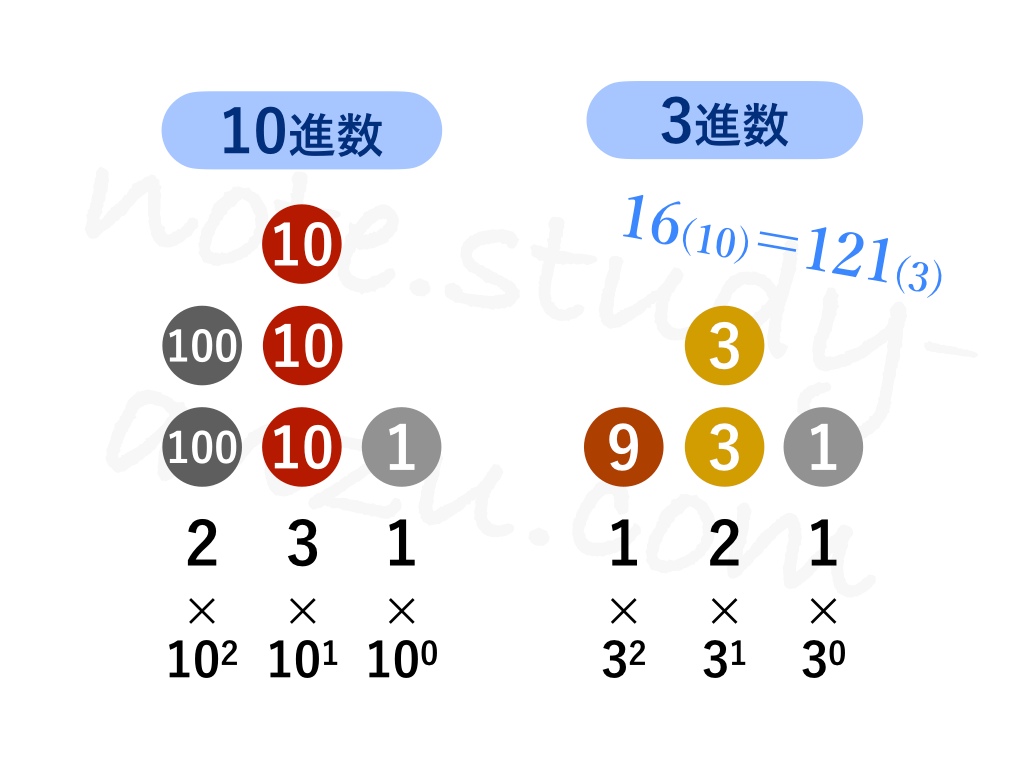
この図のように、3進法ならそれぞれの桁を3の○乗で掛け算し、それらを合計すれば10進数に変換することができます。
10進数をn進数に
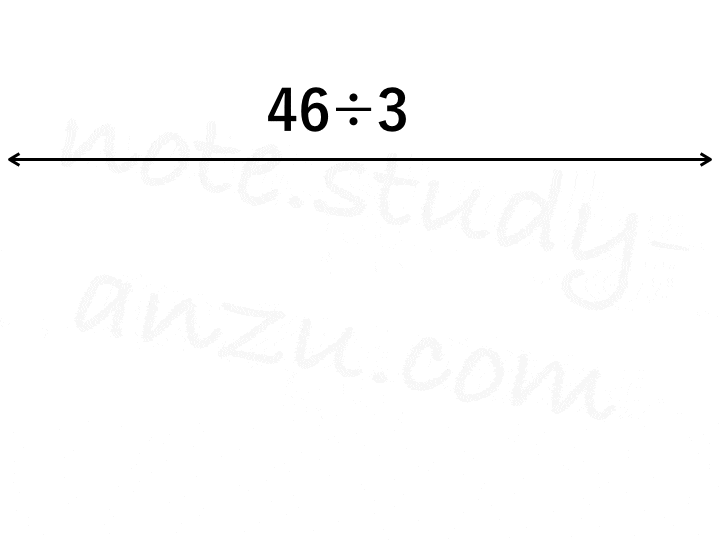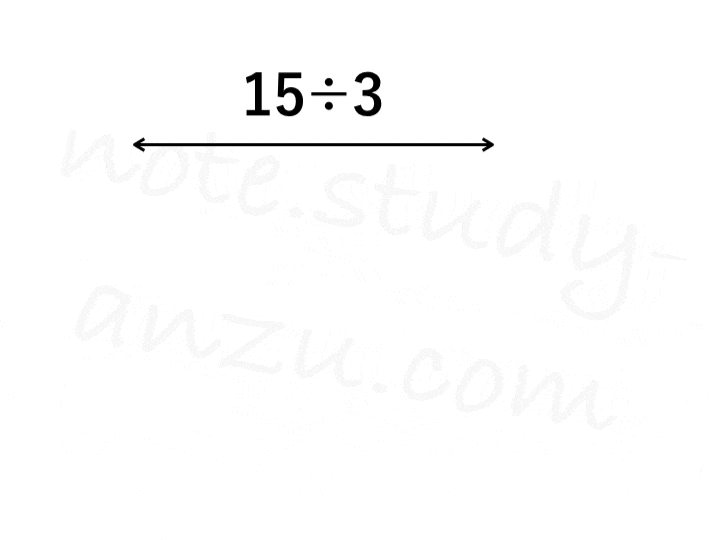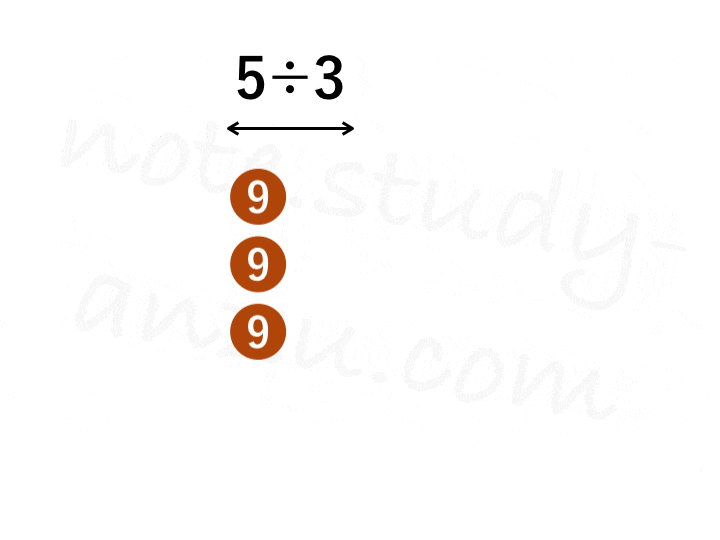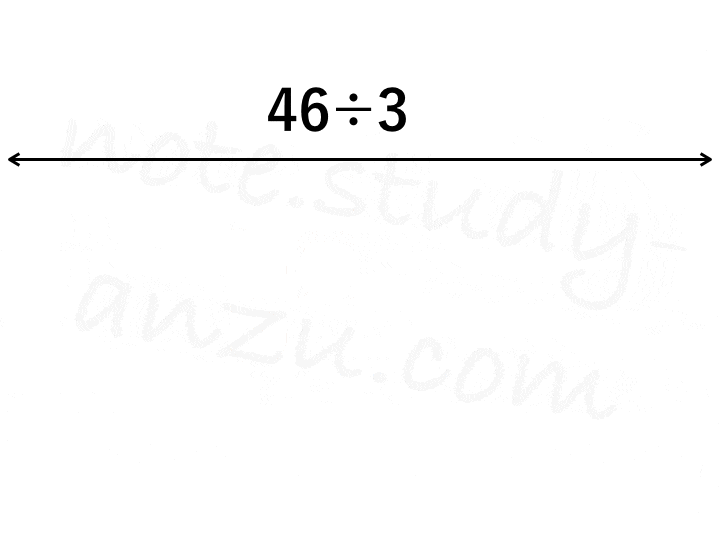
n進数から10進数への変換は、今見たようにイメージしやすいと思うのですが、その反対となるとトリッキーな作業が必要です。まずは図のアニメgifをご覧ください。10進数の46を3進数に直す方法です。
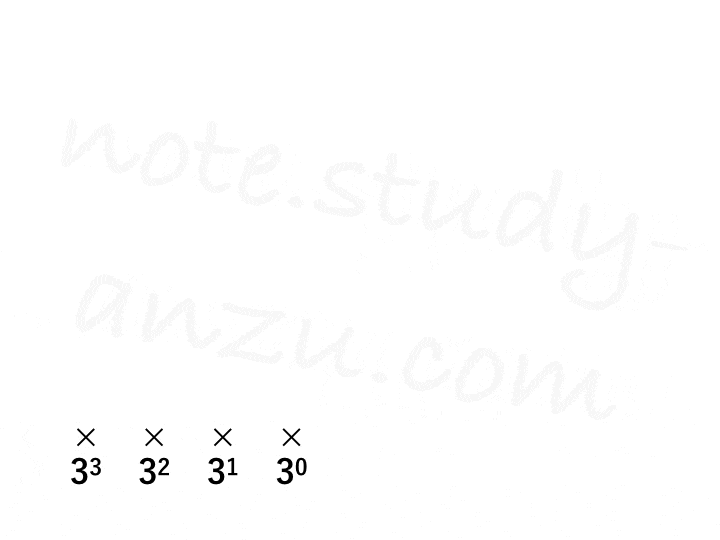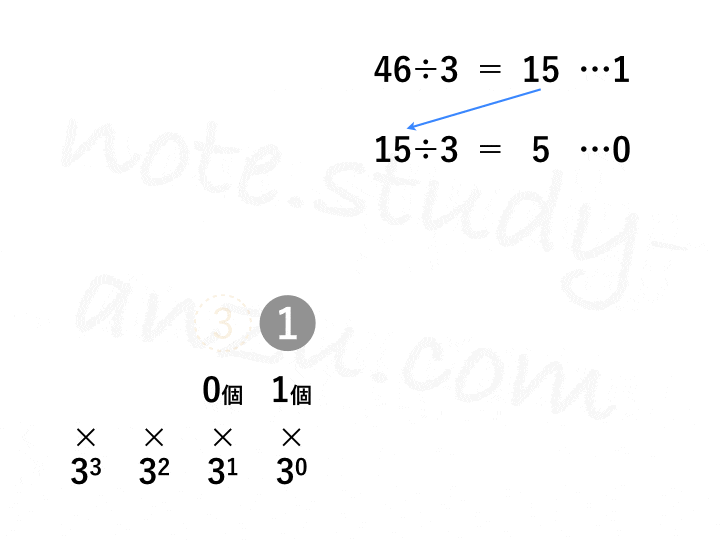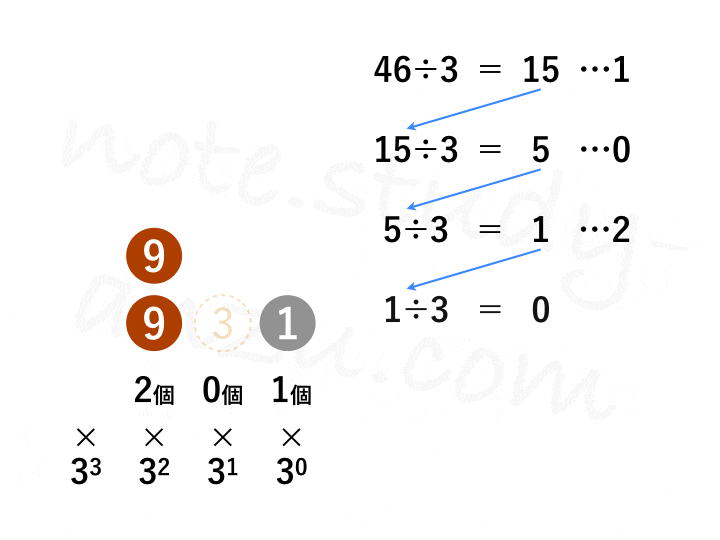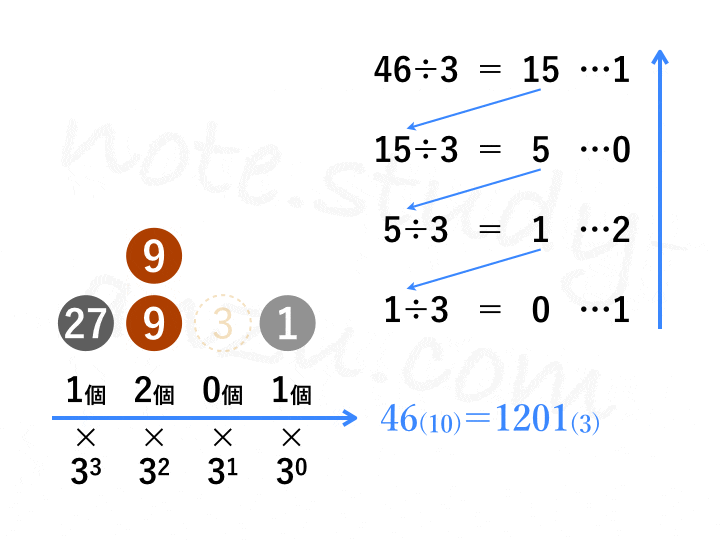
実際に計算する場合は、図の右上部分のみ書けばOKです。このように、10進数の整数をn進数に変換する場合は、nで割り算する作業を繰り返します(※小数部分は方法が違いますので、後半までお待ちください)。そのとき出て来た余りを書き並べ、下から順に読み上げていけばOKです。
手順自体は難しくないですが、なぜそんな計算で答えが出てくるのでしょう?なかなかピンとこないと思います。そこで、計算の仕組みについてがんばって図解してみます(高校のテストで出題されるわけではないですが、一応知っておけば気持ちがスッキリすると思うので……)。次の図表をどうぞ。
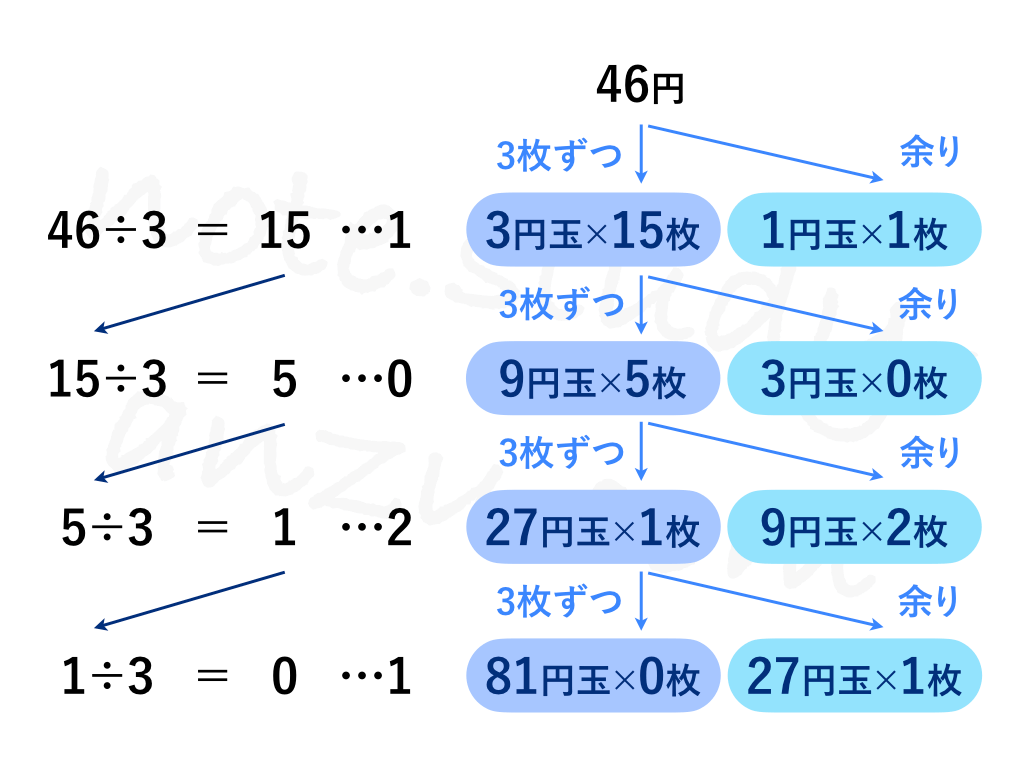
3進数というのは、コインを3個ずつまとめていく考え方になります。例えば最初の計算、46円を3で割ると、3円玉15枚にまとまりますが、余りが1つ出てくるので、これが1円玉1枚分となります。
余った1円は脇に置いておいて、次に、割り切れた15枚のコインをさらに3枚ずつまとめていきます。すると5で割り切れて余りは出ません(9円玉が5枚できることになります)。これら5枚のコインをまた3枚ずつまとめ……という作業を繰り返していき、余ったコインを積み重ねていくと先ほどの計算と同様になります。
もう1つ、解説用のgifを作りました。「3個ずつまとめる」という作業をビジュアル化してみましたが、うまく伝わりましたでしょうか。
小数の場合
この調子で、小数部分の取り扱いも見てみましょう。まず、n進数から10進数へ直す方法はそれほど難しくありません。

小数第1位はn分の1をかけ、小数第2位はnの2乗分の1をかけ……というのを繰り返します。
厄介なのが10進数からn進数への変換で、先ほどは割り算で処理しましたが、今度はかけ算で次のようにやっていきます。

この例は5進数への変換で、小数部分に5をかけて、またその小数部分に5をかけるという方法になります。小数部分がなくなったら最後の仕上げとして、かけた結果の整数部分を上から順に並べていけば作業終了となります。
テスト対策上は計算方法だけ押さえておけば十分ですが、その仕組みについても何とか解説してみたいと思います。先ほどの計算が、5進法の世界の中ではどうなっているか、並べて図表にしてみました。
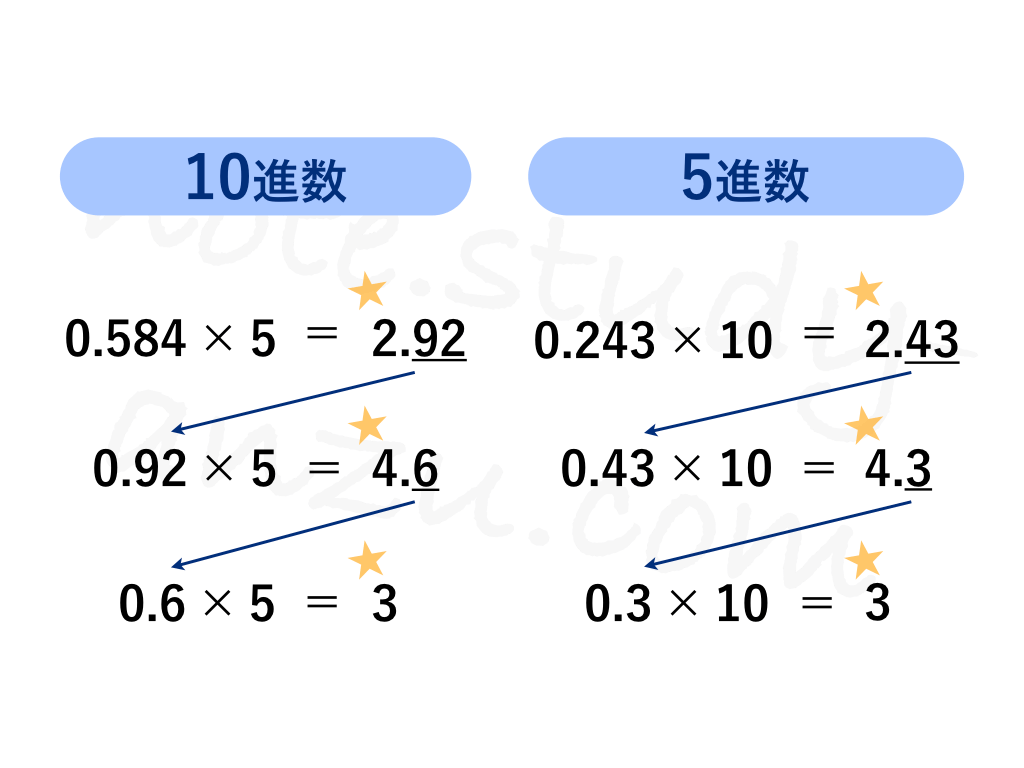
まず、5を掛け算するというプロセスですが、「5」を5進数に直すと10となりますので、5進数の世界では10の掛け算を繰り返していることになります。10をかけるということは、ケタが1個左にずれるということ。ケタを1個ずつ動かしていくことで、整数部分も1つずつ取り出せるという仕組みになっています。
具体的にはまず、0.584に5をかけると2.92という結果になり、整数部分に2が出てきました(※)。この計算は、5進数ではもとの数字に10をかけたことになりますから、小数第1位の「2」が1個分左に押し出されて、整数部分として現れたことになります。
(※念のため述べておくと、10進数の整数部分が0~4であれば、これを5進数に変換しても整数部分は同じ数字になります。)
そして、整数部分の2を差し引いた、0.92という数字に5をかけると4.6になります。この整数部分の「4」という数字は、もとの数字(5進数)の小数第2位にあたります。これ以降も同じ処理でやっていきます。
というわけで、10進数の小数部分を変換させる作業については、「ケタを1個ずつプッシュしていく」というイメージで考えればよいことになります。