集合の要素の個数の最大・最小(黄チャート重要例題)
「黄チャート」の集合(数学A)に関する重要例題で、要素の個数の最大最小を求める問題があります。チャートによる解説がとても抽象的でイメージしにくく、説明に苦労しましたので、ここで図表を作って確認してみたいと思います。問題の概要は次の通り。
- 海外旅行者100人中、カゼ薬持ちは75人、胃薬持ちは80人。
- 両方持ちの人数m人としたとき、mの最大値・最小値を求めよ
考え方はとてもシンプル
カゼ薬持ち、胃薬持ちの集合をそれぞれA, Bとします。
今回は、「AかつB」についての最大・最小を求める問題ですが、「AかつB」の最大最小と「AまたはB」の最大最小は反対になるイメージを持っていくと解きやすいです。下の図をご覧ください。
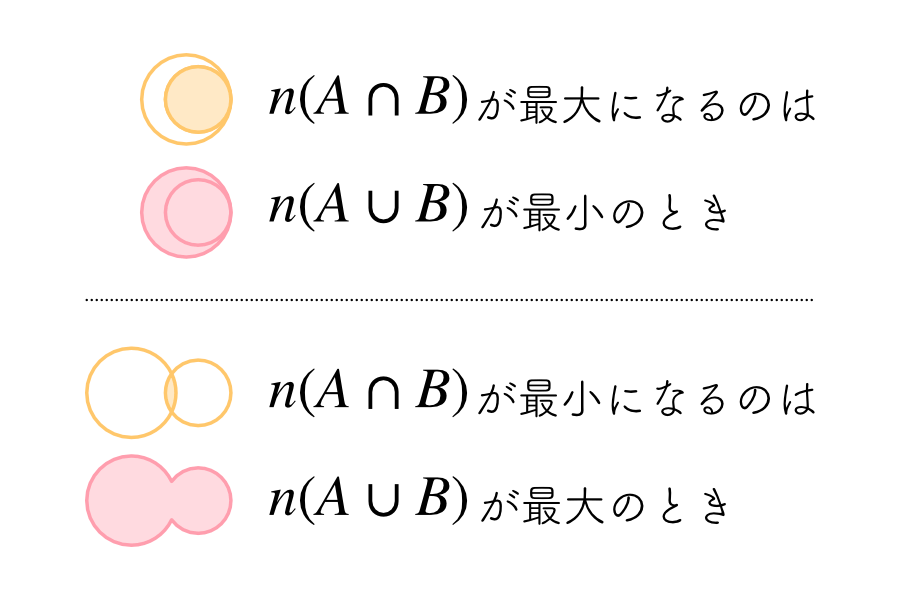
「AかつB」が最大というのは、ベン図の2つの円の重なりができるだけ多くなればいいわけです。大きな円の中に小さな円がすっぽり入る(A⊂B)状態を考えてみてください。重なりが多い分だけ、「AまたはB」を表す範囲は小さくまとまります。
反対に「AかつB」が最小になるとき、2つの円の重なりあう範囲はゼロか、あるいはとても小さくなります。このとき「AまたはB」の示す領域は最大となり、2つの円がヒョウタンや雪だるまのように並んでいる形をイメージすればOKです。
問題に当てはめる
では、具体的に今回の問題に当てはめて考えてみましょう。「AかつB」に属する人数(m)を求めるため、集合分野ではおなじみの「個数定理」を使っていきます。具体的には、AとBに属するそれぞれの人数を単純に足し合わせると155人となりますが、そこから「AまたはB」の分を引き算すると、「AかつB」の人数が求められます。
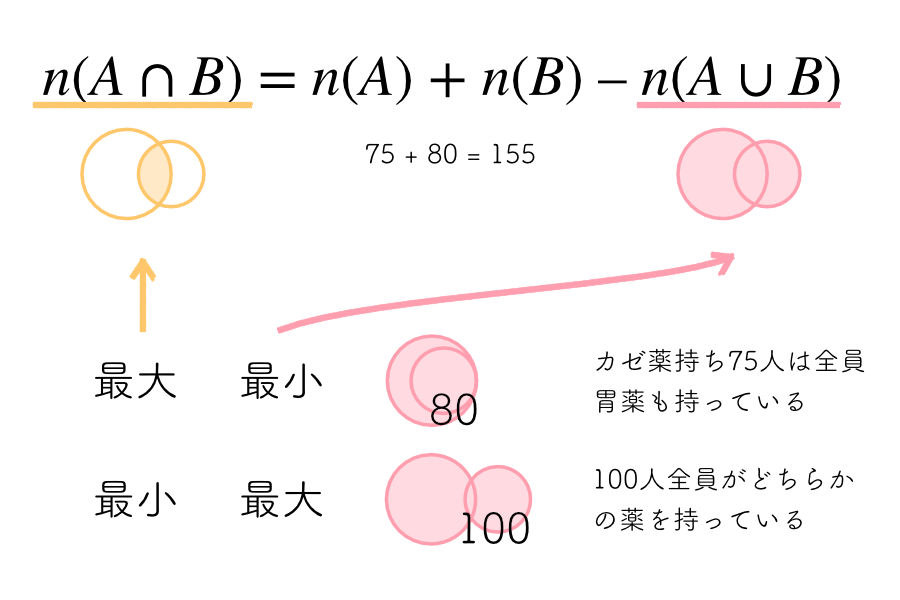
「AかつB」が最大のときはイメージしやすいと思います。2つの集合の重なりあう範囲が最大になるわけで、カゼ薬を持っている全員が胃薬持ち80人の中に含まれていると考えればOKです。よって、mの最大値は
m = 155 – 80 = 75
「AかつB」が最小をとるとき、「AまたはB」は反対に最大値となります。今回のケースでは、100人全員が「AまたはB」に属していればOKで、具体的には旅行者100人全員がどちらかの薬を持っていることになります。よってmの最小値は
m = 155 – 100 = 55
です。